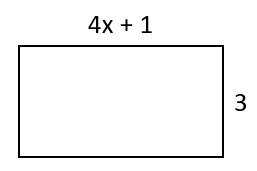Algebra is a wonderful thing, if we know how to use it correctly.
One of its major advantages is that it allows us to work with numbers which we don't know; we call these variables.
The technique we will discuss today is how to create and solve an equation to find one of these things that we don't know.
e.g. A rectangle has sides of (4x + 1) cm and 3 cm.
It also has a perimeter of 16cm2.
Find the area of this rectangle.
This question is a perfect example of using an equation to solve a problem.
The thing that gives it away is that we are asked for something which is currently an unknown (x).
Step 1: Draw a diagram to help you if possible (or if you aren't already given one):
Step 2: Create an expression for the elements you know.
In this question, we are given the perimeter.
We know that perimeter is calculated by adding the sides together so let's do that with the algebra:
(4x + 1) + 3 + (4x + 1) + 3
8x + 8
It's worth noting that we have not made this into an equation.
This is only because the question asks for an expression on this occasion.
Step 3: Create an equation for the elements you know.
We have just worked out an expression for the perimeter, and we know that the perimeter is equal to 16.
This gives us the equation then:
8x + 8 = 16
Step 4: Solve the equation.
We can just do this using our basic equation rules: do the same to both sides, and apply the opposite operation.
8x + 8 = 16
8x + 8 - 8 = 16 - 8
8x = 8
8x ÷ 8 = 8 ÷ 8
x = 1
Step 5: Answer the question that was asked.
In this question, we are asked to find the area.
To do this, we need to find the lengths of the sides and then multiply them together.
Remember that we just calculated that x = 1.
Side 1: 4x + 1 --> 4(1) + 1 = 5 cm
Side 2: 3 cm
Therefore, we can see that the area of this rectangle is 5 × 3 = 15 cm2
In this activity, we will create expressions and equations based on problems then solve them to find variables and apply this knowledge to calculate new information.