Did you play one of these at school when you were younger?

 

 

The good old days of the triangle before they became bothersome in maths questions.

 

What examples can you think of that we see in everyday life?

 

 

Builders may need to know about triangles for working out the areas of gable ends of houses.

You might need to know the area for cutting patterns in the shape of a triangle to make bunting, or make a kite.

Before we can do any of these, there is one thing we need to know, and that is how to find the area of a triangle.

 

First, we are going back to look at how to find the area of a square and rectangle.  Why?  It might help you to understand and remember the formula for the area of a triangle.

 

 

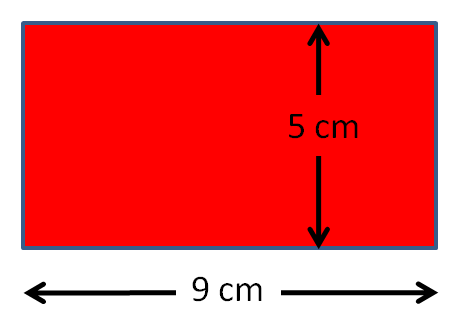
Area of a rectangle = base x height

 

 

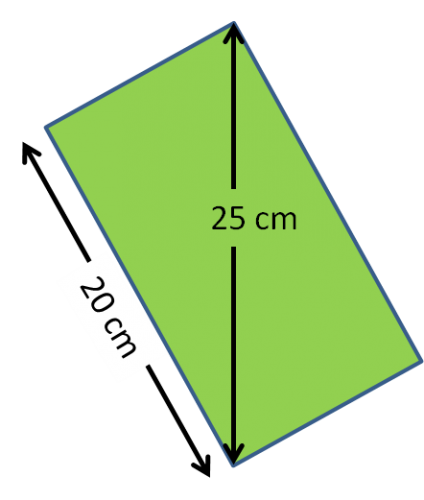
In the diagram above, look what happens when a diagonal line is drawn from one corner of the rectangle to the other.  By cutting it in half, I have made two triangles. Cutting it in half is the same as dividing by 2.

 

The area of each half, or each triangle = base x height ÷ 2

or another way of writing this is:

Area = 1/2 base x height

 

 

Now you could go barking up the wrong tree, so be careful!

When you are given measurements for a triangle, you are sometimes given the base, vertical height and a slanted height.  

You always want the vertical height.

 

 

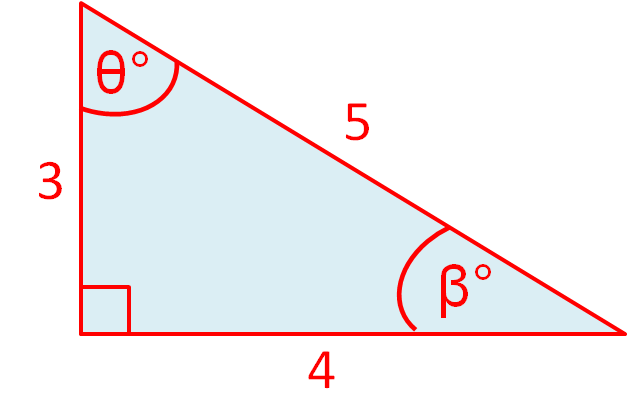
To find the area of this triangle we need to know the base of 4 x vertical height of 3 = 12

12 ÷ 2 = 6 units²  

 

Once you have learned the formula you are flying!