Parallelogram - another two dimensional shape that we might easily recognise, but not always remember its name.

 

It has opposite parallel sides, which may help with remembering the name.

 

 

What examples can you think of that we might see in everyday life?

 

 

Believe it or not, you can be two things at once!

 

For example, a square has two sets of parallel sides, so it is also a parallelogram but we call it a square. The same goes for a rectangle.

Basically, a parallelogram is a four-sided shape with opposite sides parallel and equal in length (the same as a square or rectangle).

 

 

Mathematicians can be awkward and make a four-sided shape look different just for fun, so that's how we arrive at parallelogram.

There are all sorts of reasons we might need to know the area of a parallelogram. So how do we do that?

 

First of all, we know that the sides of a parallelogram are not always the same length. 

Two sides will have one length and the other two sides might have a different length.

 

As with a lot of shape work, there is a formula that you need to learn. So here goes:

 

Area of a parallelogram = base x height

 

You may recognise that it is the same as the formula for the area of a square and a rectangle.

 

Find the area of the parallelogram below:

 

 

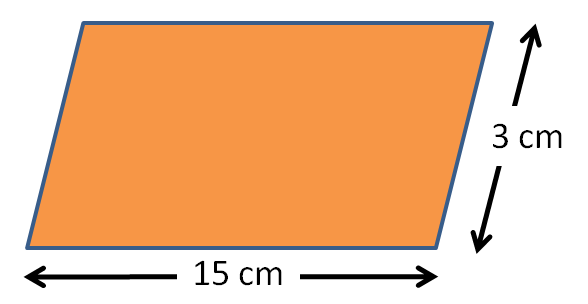
Area = base x height

Hang on!! We cannot work out the area of the parallelogram above as we only know the slanted height!

 

Let's try this one instead.

 

 

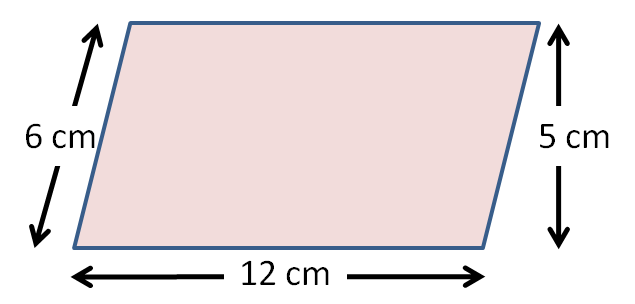
 Look out!  You need to work with the vertical height, not the slanted height.

12 x 5 = 60 cm²

 

As we are working with area, units are always squared. e.g cm², m²

 

What a bargain - one formula for three shapes.