In this activity, you will be asked to think about coordinates on a positive and negative axis using a coordinate grid.
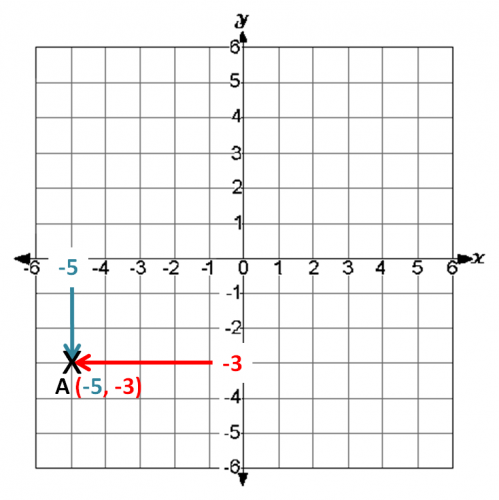
Remember, we always read along the corridor (the x-axis) and then up/ down the stairs (the y-axis).
Look at the point A...
Its x-coordinate is -5 on the x-axis.
Its y-coordinate is -3 on the y-axis.
The x number always comes before the y number.
We write the coordinates for A as (-5, -3)
Notice, we always write coordinates in brackets with a comma between the two numbers.
Using the rules above, check you can read each of the points of the parallelogram on the coordinate grid.
Remember, 'along the corridor and up/down the stairs'
You always write the x point before the y point.
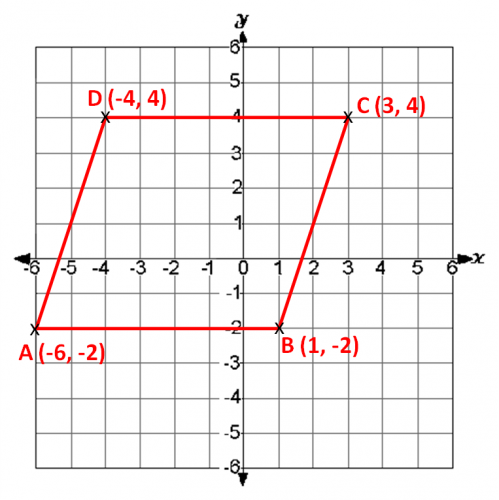
Do you notice with the parallelogram above, that the shape crosses both the x-axis and the y-axis? We can see this from the grid above, but we could also tell this even without an image by looking at the coordinates.
Point D is on the left side of the y-axis with the x-coordinate as a negative number (-4). Point C however, is on the right side of the y-axis with a positive x-coordinate( 3) . If the x-coordinates are a mixture of positive and negative numbers, then the shape must be crossing the y-axis.
We can see that the shape is also crossing the x-axis because point A has a negative y-coordinate (-2) and point D has a positive y-coordinate (4). If the y-coordinates are a mixture of positive and negative numbers, then the shape must be crossing the x-axis.

One other skill that we will be testing in this activity is working out the midpoint of a line.
If we take the line D-C above, we can work out the midpoint of the line by looking at the coordinates.
D is (-4, 4) and C is (3, 4). The line is horizontal, so we only need to look at the x-coordinates.
We need to find halfway between the coordinates -4 and 3. The difference between -4 and 3 is 7.
We divide 7 by 2 to find the midpoint of the line: 7 ÷ 2 = 3.5
The midpoint of line D-C is 3.5
We can also find the midpoint of line C-B
The coordinates of C are (3, 4) and B are (1, -2)
This line is diagonal, so we need to look at both the x and y-coordinates.
First, the x-coordinates.We have 3 and 1. The number 2 will be exactly in the middle, so that is the x-coordinate of the midpoint.
Now, the y-coordinates. We have 4 and -2. The difference between these is 6. We have to find the midpoint between them by dividing 6 by 2 and then adding that onto the smaller coordinate.
6 ÷ 2 = 3
-2 + 3 = 1
So, the y-coordinate for the midpoint will be 1
The midpoint of the line C-B is (2, 1)
There's a lot to think about in these questions, so remember that you can just click on the red help button on the screen to see this introduction again.

Let's get started.







