Find the Sum of Interior Angles

 You already know that the interior angles of a triangle add up to 180º.

 

 

Polygons with more sides have a larger sum of interior angles.

 

There is a lovely little formula to use to find out the sum of the interior angle of any polygon.

 

Here it is:

Where n is the number of sides of a polygon: (n - 2) x 180 = the sum of the interior angles.

 

Let's test it out with some polygons:

Triangle has 3 sides: (3 - 2) x 180 = 1: x 180 = 180

Quadrilateral has 4 sides: (4 - 2) x 180 = 2 x 180 = 360

Pentagon has 5 sides: (5 - 2) x 180 = 3 x 180 = 540

Hexagon has 6 sides: (6 - 2) x 180 = 4 x 180 = 720

Octagon has 8 sides (8 - 2) x 180 = 6 x 180 = 1,080

 

Does that make sense?

 

This means that if we know the number of sides a shape has, we can work out the sum of the interior angles. If we know the sum of the angles, we can also work out one individual angle if the polygon is regular, with all its angles the same size.

 

If we know the sum of the interior angles, we can work out how many sides the shape has by dividing the sum by 180. For example, if we know that the sum of a polygon's interior angles is 900, we simply divide 900 by 180.

900 ÷ 180 = 5.

Add on 2: 5 + 2 = 7

and we know that the shape must be a 7-sided shape - a heptagon.

 

Shall we move on to some questions now?

 

If you want to understand more about how the formula works, then you can read the explanation below, but you don't need to know this, so long as you remember the formula;

(n - 2) x 180

 

Extra information if you want to know more!!

To work out the sum of the interior angles of a polygon with more sides, we choose one of the corners and split the polygon into triangles.  Each triangle will contain 180°.

 

Example

Work out the sum of the interior angles of this hexagon.

 

 

Answer

Choose any one corner.

 

 

Draw diagonals from the chosen corner to form triangles.

 

 

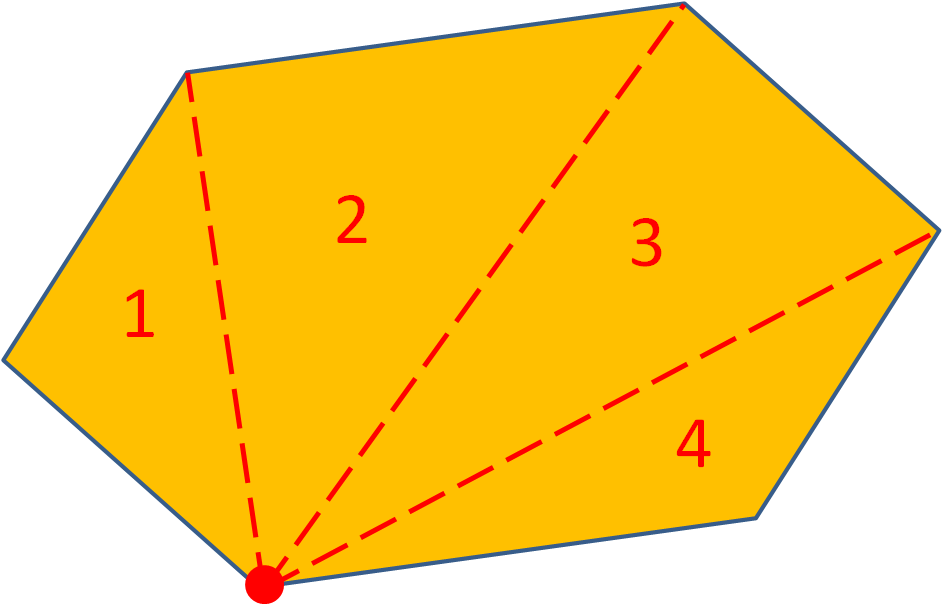
There are 4 triangles inside the hexagon.

4 x 180° = 720°

 

The sum of the interior angles of a hexagon is 720°.

 

General Rule:

When you have a shape with n sides, the number of triangles it can be split into is n - 2

Once you have the number of triangles, we can simply multiply that by 180° to find the internal angles.

For example: A 5 sided shape can be split into 3 triangles, if you then multiply 3 by 180 you get that there are 540° in a 5 sided shape.