Loading please wait

The smart way to improve grades

Comprehensive & curriculum aligned

Try an activity or get started for free

  1. Maths
  2. Year 9
  3. Algebra: Expressions
left-icon BACK TO WORKSHEETS

Algebra: Cube Roots of Algebraic Terms

In this worksheet, students simplify the cube roots of algebraic terms.

'Algebra: Cube Roots of Algebraic Terms' worksheet

Key stage:  KS 3

Curriculum topic:   Algebra

Curriculum subtopic:   Use and Interpret Algebraic Notation

Difficulty level:  

---- OR ---- Preview Activity

Worksheet Overview

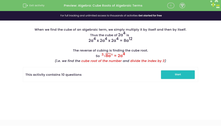
When we find the cube of an algebraic term, we simply multiply it by itself and then by itself.

Thus the cube of 2a4 is  

2a4 x 2a4 x 2a4 = 8a12

 

The reverse of cubing is finding the cube root.

So  3√8a12 = 2a4

(i.e. we find the cube root of the number and divide the index by 3)

---- OR ----

Preview activity

What is EdPlace?

We're your National Curriculum aligned online education content provider helping each child succeed in English, maths and science from year 1 to GCSE. With an EdPlace account you’ll be able to track and measure progress, helping each child achieve their best. We build confidence and attainment by personalising each child’s learning at a level that suits them.

Get started
laptop

Similar activities you may like

Try an activity or get started for free