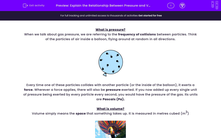
What is pressure?
When we talk about gas pressure, we are referring to the frequency of collisions between particles. Think of the particles of air inside a balloon, flying around at random in all directions.
Every time one of these particles collides with another particle (or the inside of the balloon), it exerts a force. Wherever a force applies, there will also be pressure exerted. If you now added up every single unit of pressure being exerted by every particle every second, you would have the pressure of the gas. Its units are Pascals (Pa).
What is volume?
Volume simply means the space that something takes up. It is measured in metres cubed (m3)

For example, a hot air balloon has a much greater volume than a party balloon as it is much larger.
It is important to understand that the volume of a gas depends on the space between the particles, not the size of the particles themselves. Gases with larger volumes have more spaced-out particles than gases with small volumes. It isn't caused by the gas being made out of bigger particles.
If volume changes, what happens to pressure?
Now, it's time to learn some maths skills! But first, let's look at the physics behind it.
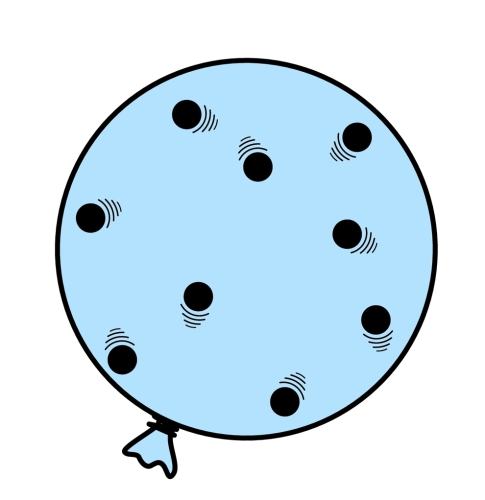
Look at the two balloons below:
The balloon on the right has a larger volume than the balloon on the left. Notice that we are keeping the number of particles equal (and of course the size of the particles is also the same for both balloons). Also, to make this a fair comparison, we will also keep the temperature of both balloons the same, to ensure that all the particles are moving at the same speed.
Which balloon will have the greater pressure? If you consider that pressure depends on the number of collisions every second, the answer is of course the balloon on the left. This is because, every second, there will be more collisions occurring as the particles have less space to move around in. Meanwhile, giving the particles more room to move around will mean that they will have less chance of colliding, and so the pressure will be lower.
Essentially, decreasing the volume increases the pressure (and increasing the volume decreases the pressure).
What if we plotted this on a graph?
If you now carried out an experiment on pressure and volume and plotted your results on a graph, you would get the following:
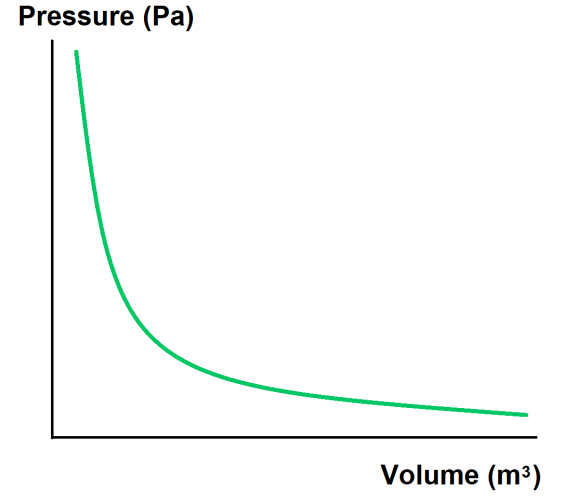
As you can see, the graph is a curve. To be more precise, the pressure is inversely proportional to volume.
This means that the relationship is more than just 'as one increases, the other decreases'. It means that the two values will always multiply together to make the same number. Or, think of it this way: whatever you multiply one of the values by, you must divide the other value by the same amount.
Let's do an example to make sense of this:
The original pressure of a gas is 2 Pa and its volume is 12 m3
If its pressure increases to 6 Pa, its new volume must become 4 m3
Why?

If we look at the original pressure and volume, they multiply together to make 24 (by simply doing 2 x 12)
It means the final pressure and volume must also multiply to make 24, and this is the case (6 x 4 = 24)
Here's another way to look at it:
The pressure has multiplied by 3. (It was 2 Pa, and now it is 6 Pa).
As pressure and volume are inversely proportional, it means that the volume must now be divided by 3.
12 m3 ÷ 3 = 4 m3
This method allows you to calculate a new pressure or a new volume if one of those factors changes.
Remember, the law that pressure is inversely to volume only applies if the temperature of the gas, and the number of particles of gas, remain constant.
Have a go at some questions on this topic and see how you get on.