What would you rather be hit by, a speeding feather or a speeding train?
.jpg)

It’s the feather, right? But why? We'll be looking at kinetic energy in this activity and by the end of it, you should be able to remember, use and rearrange the equation for kinetic energy to solve complex problems.
(A heads up - this activity will assume you know how to rearrange equations and have a good mathematical understanding of applying them).
Are you ready? Let’s get stuck in!
As you should already know, kinetic energy is how moving things store their energy. There are a few things that affect this and we'll be using the idea of the feather and the train to try and understand the different factors that affect kinetic energy.
Why would you rather be hit by a feather? Because it’s light, right? This is true, the mass of the object will affect how much kinetic energy it has. The more massive an object, the more energy it will have. Let’s make a note of this.
Energy (E) ∝ mass (m)
That fancy sign in the above equation (∝), is called the proportional sign. When something is proportional, it means that if one thing goes up, then the other must go up as well. Here, this means that if we change the mass, we also change the energy.
Let’s change the situation a little bit now. The train is moving at 0.01 m/s and the feather is moving at 1,000 m/s. Which one would you rather be hit by now? Did you go for the train? That’s because speed (or velocity) also has an effect on the kinetic energy (if you want to know more on this and why this works, have a look at our activity on momentum - it will explain this in a lot more detail). Let’s add this to our proportionality:
Energy (E) ∝ mass (m) x velocity (v)
All we're saying here is that if we change either the mass or the velocity, then it will affect how much energy there is. If either of them goes up, then the energy will also go up - the same applies if they go down.
Oh – but it isn’t as simple as that… scientists have conducted experiments and found that one of these things has a much more significant effect on energy than the other. When we draw graphs of energy against mass and velocity, we find that the mass graph forms a line of about y = ½ x and the velocity graph looks like a y = x² graph!
By using these two graphs, we know that the mass has to be halved and the velocity needs to be squared. This leads us to the equation - we have to halve the mass and square the velocity, so the equation looks like this:
.
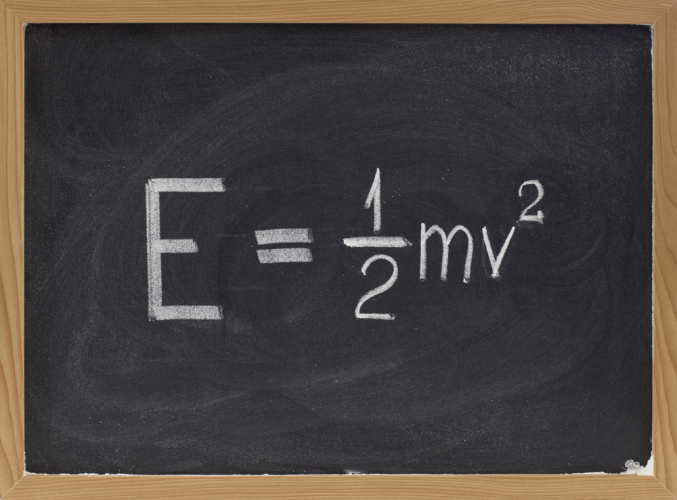
Fun fact time! You have to remember this equation - you will not be given it in the exam.
So how do you use this equation? Simple! Let’s go through an example together - this is where the maths comes into play!
Jim is an expert at throwing. He can literally throw anything (including a tantrum) using a specific amount of energy - it is always 500 J. One day, he throws a ball at a speed of 5 m/s. Calculate the mass of the ball.
Step 1 Find the values that matter to you in this question and highlight them:
Jim is an expert at throwing. He can literally throw anything (including a tantrum) using a specific amount of energy - it is always 500 J. One day, he throws a ball at 5 m/s. Calculate the mass of the ball.
Step 2 Work out if you need to rearrange the equation:
In this example, we need to rearrange for mass.
The equation is currently E = ½mv²
Firstly, multiply out the ½
Then, divide by the v²
This makes mass the subject of the equation: m = 2E ÷ v²
Step 3 Put these values into the equation:
m = (2 x 500) ÷ 5²
Step 4 Put these into your calculator and press =
m = 40 kg (it's a heavy ball)
Step 5 Round if you need to. Normally we round to 1 decimal place (dp) or 2 significant figures (sf) unless the question tells you otherwise!
No rounding is needed in this answer.
Don’t forget the unit of energy is the joule (J)!
Now let's try some questions.







