Calculate Areas: Triangles

Use the following formula to work out the area of a rectangle:

 

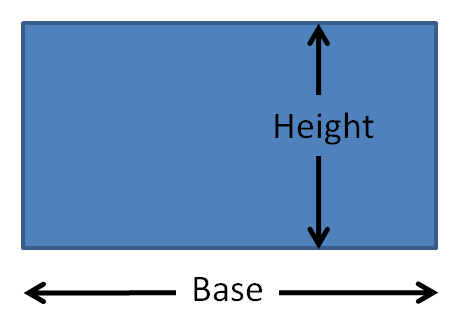
We must know:

• the base length
• the perpendicular height from the base to the top.

 

Area of rectangle = base × height

 

 

Now, try this with a piece of paper.

Start with a rectangle.

 

Cut off a right-angled triangle from the left-hand side and separate the two pieces.

The area of the two pieces together will be the same as the original rectangle.

 

Cut off a right-angled triangle from the right-hand side to form a triangle in the middle, and separate the three pieces.

The area of the three pieces will still be the same as the original rectangle.

 

Now look carefully at the pieces marked A and B below.

Notice that the areas match. 

A matches A and B matches B.

 

So the area of the triangle in the middle is half the area of the rectangle.

 

 

Area of Triangles

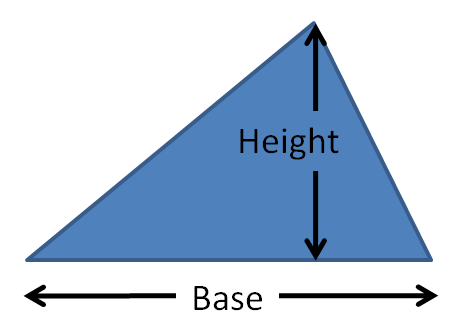
We must know:

• the base length
• the perpendicular height from the base to the apex. (NOT the slant heights)

 

Area of triangle = ½ base × height

or

Area of triangle = base × height ÷ 2

 

 

Example

Calculate the area of this triangle in cm².

 

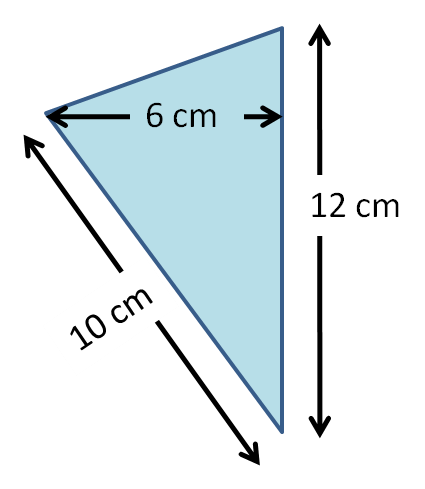
Answer

This is a triangle.

We must know:

• the base length
• the perpendicular height from the base to the top. (NOT the slant height)

 

If we turn our heads to the left, the base length is 12 cm and the perpendicular height is 6 cm.

We do not need to know the slant height of 10 cm to use the formula.

 

Now we use the area formula:

Area of triangle = ½ base × height

Area = ½ × 12 × 6 = 6 × 6  =  36 cm²

 

Or...

 

Area of triangle = base × height ÷ 2

Area = 12 × 6  ÷ 2 = 72 ÷ 2 =  36 cm²