Look at the following diagram.
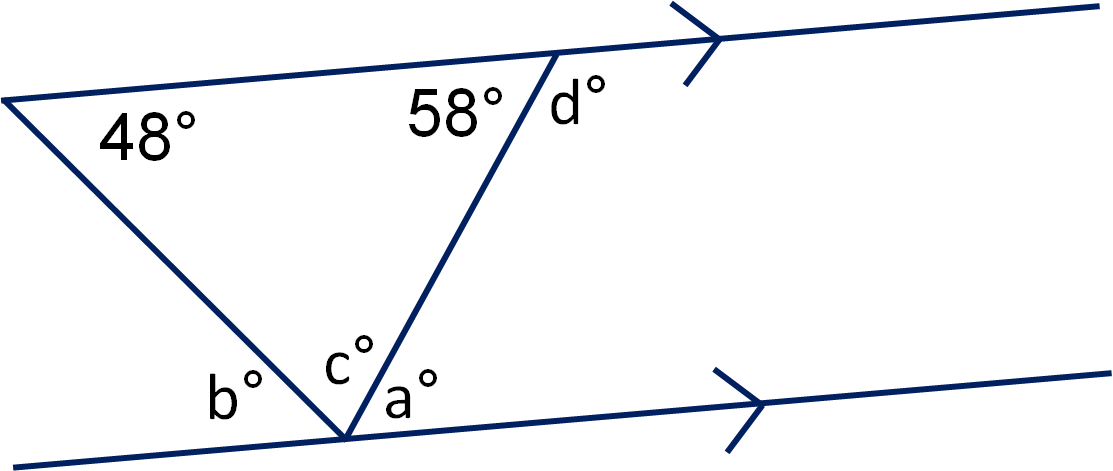
Angle a° = 58° because it is alternate to the 58° on parallel lines (Z or S shape)
Angle b° = 48° because it is alternate to the 48° on parallel lines (Z or S shape)
Angle c° = 180° - 48° - 58° = 74° for two reasons.....angles in a triangle add up to 180° and angles on a straight line add up to 180°
Angle d° = 180° - 58° = 122° because angles on a straight line add up to 180°








