Irregular shapes have sides and angles of any length and size.
The area of a shape is the amount of space taken up by a 2D shape or surface.
We measure the area in either cm² or m².
When we have a regular shape, we can calculate the area using the formula length x width.
However, when we have an irregular shape, we can estimate the answer by counting the number of squares it covers.
e.g. Look at the shape below:
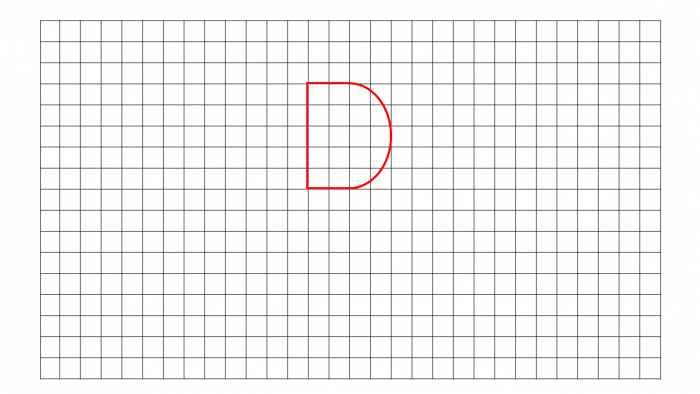
In order to find the area of this shape, follow these steps:
1. Count the complete squares as one.
2. Count squares covered more than half as one.
3. Ignore the squares that are covered less than half.
4. Add together the number of complete squares and squares covered half or more.
By doing this, we can then find an 'approximate' area.
Complete squares = 13
Squares covered more than half = 5
Approx Total Area = 18 cm²








