Convert Improper Fractions to Mixed Numbers

In this activity, we will be learning about mixed numbers and improper fractions. 

A mixed number is made up of a whole number and a fraction.

Let's look at the mixed number below:

This is 3 wholes and 2 fifths.

3 wholes are the same as 5 fifths + 5 fifths + 5 fifths = 15 fifths.

15 fifths + 2 fifths = 17 fifths in total.

Have a look at this picture to help you visualise it:

A quick way to work this out is: 3 x 5 + 2 = 17

Can you see how you multiply the whole number (3) by the denominator (5) and then add the numerator (2)?

3 x 5 = 15 + 2 = 17

17/5 is an improper fraction because it is top-heavy. 

That means that the top number is bigger than the bottom number.

It is also easy to convert an improper fraction into a mixed number.

Look at the improper fraction below:

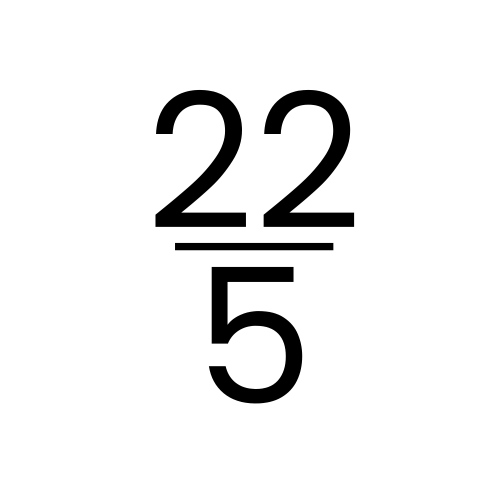
We know that there are five fifths in every whole number, so we can convert this into a mixed number if we divide the numerator by the denominator:

22 ÷ 5 = 4 remainder 2.

So, we have 4 whole numbers and 2 fifths left over as the remainder.

We write the remainder as the numerator. This gives us the answer of 4 and  2/5

We are going to practise converting improper fractions into mixed numbers in this activity. You can look back at this example at any point by clicking on the red help button on the screen.

Let's get started!