In this activity, we'll be tackling the topic of adding and subtracting fractions with different denominators.
What does this yummy looking chocolate cake have to do with fractions? See if you can work it out!

Hopefully, we already know that you can't add fractions with different denominators.
A denominator tells us how many equal pieces make one whole. If you add the denominators when adding fractions, the new denominator won't describe how many equal pieces are in one whole.
So, we tackle this problem by finding the lowest common multiple to make both denominators the same.
Let's attempt one together:
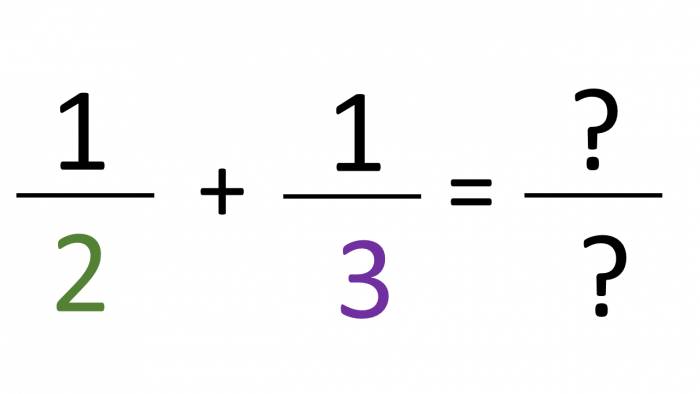
First, we look at the different denominators and we must find the lowest common multiple of 2 and 3.
1 × 2 = 2
2 × 2 = 4
3 × 2 = 6
1 × 3 = 3
2 × 3 = 6
So, we've found that our lowest common multiple is 6.
Now, we need to make both our denominators 6. The key rule to remember here is that whatever you do to the denominator, you must also do to the numerator.
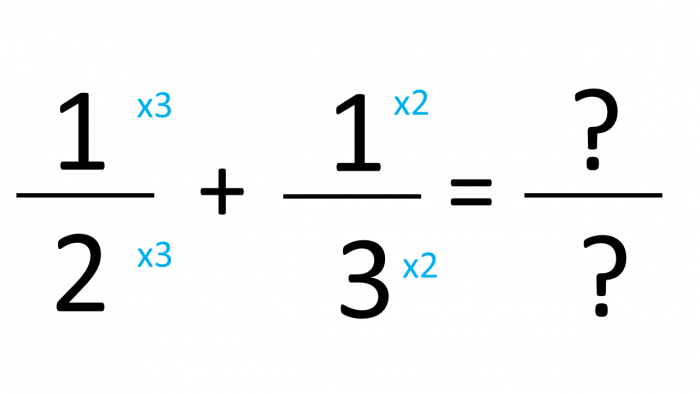
So, if we apply the calculations above we end up with:
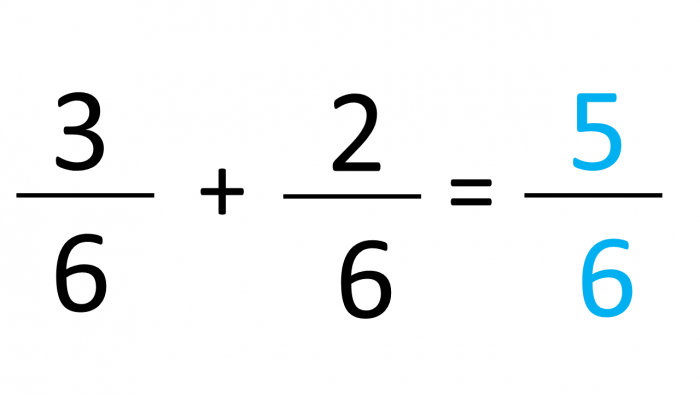
Pretty simple right?
Now it's over to you. You can always return to this explanation if you get stuck, by clicking on the red button at the side of the screen.
Good luck!








