Identify Parallel and Perpendicular Lines

In this activity, we will build on what we know about parallel and perpendicular lines.

 

We know that a straight line graph is in the form:

y = mx + c

where m is the gradient and C is the y-intercept.

 

Parallel lines

Parallel lines have the same gradient.

All of these lines have a gradient of 5.

 

 

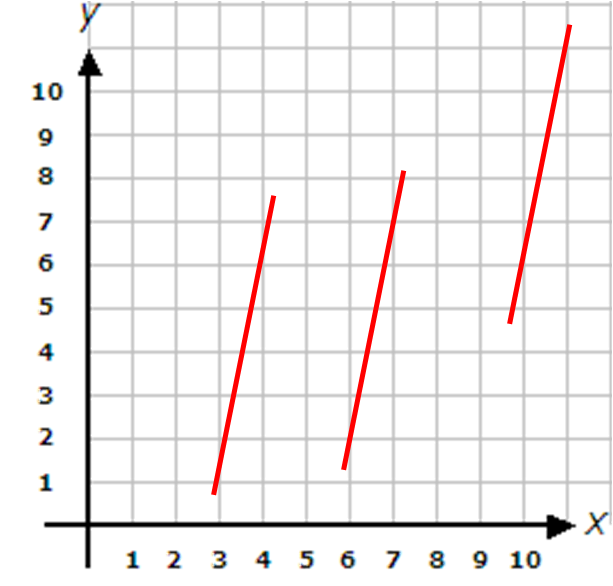
 Perpendicular Lines

Perpendicular lines have gradients which multiply together to give -1.

Here, one line has a gradient of 5 and the other of -1/5.

 

 

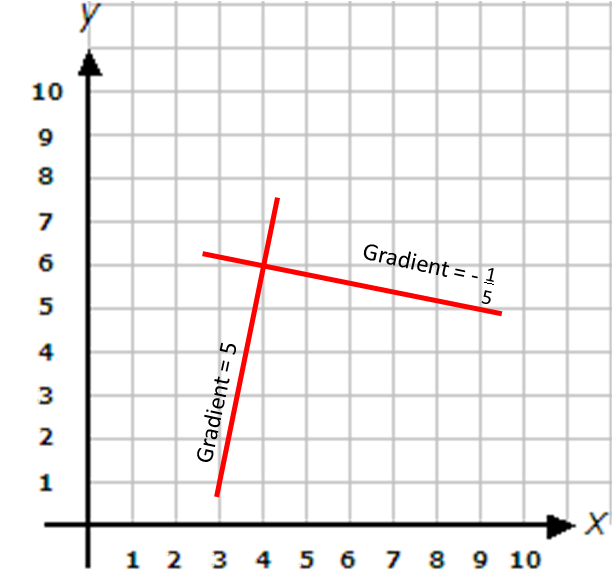
To find the gradient of a line which is perpendicular to one of gradient a/b, we invert the fraction and multiply by -1.

This is called the 'negative reciprocal'.

 

 

Don't worry - it's easier than it sounds!

 

We are going to use all this information to find straight lines which are parallel and perpendicular!

Let's look at a typical question!

 

Example

State the straight line which is parallel to 

y = 2x + 5

and goes through the point (0, 3)

 

Answer

From the straight line 

y = 2x + 5

We can see that the gradient m is 2

For a line to be parallel, it must have the same gradient.

y = 2x + C will be parallel.

 

Our line also passes through (0, 3) which is the y-intercept C

Therefore, the answer is:

y = 2x + 3

 

We do exactly the same for a perpendicular line, but instead of the gradient m repeated we find the negative reciprocal.

That is the inverse and x by -1

So, if the gradient was 2, then the perpendicular gradient is -1/2

 

 

Let's try some questions!