BACK TO WORKSHEETS
It is possible to work out the gradient of a straight line from the coordinates of any two points which lie on the line, either by drawing the line or simply by subtracting and dividing coordinates.
| Gradient of line = | y-step |
| x-step |
Example
Find the gradient of the straight line which passes through (2, 5) and (5, 9)
Answer 1
Let's look at the line drawn on a set of x-y coordinate axes.
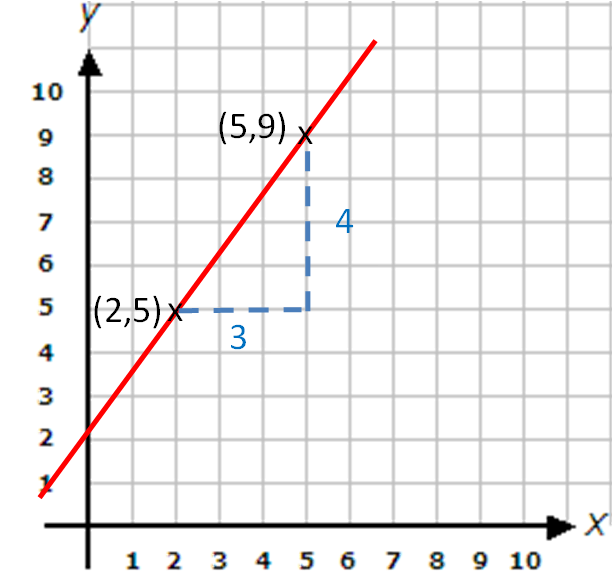
The vertical part of the step (y-step) = 4
The horizontal part of the step (x-step) = 3
| Gradient of line = | y-step | = | 4 | |
| x-step | 3 |
Answer 2
It is possible to work out the gradient WITHOUT drawing the line.
Look at the coordinates of the two points (2, 5) and (5, 9).
We can get the y-step by subtracting the y-coordinates.
y-step = 9- 5 = 4
In the same order, we get the x-step by subtracting the x-coordinates:
x-step = 5 - 2 = 3
| Gradient of line = | y-step | = | 4 | |
| x-step | 3 |
NB: We could have worked out 5 - 9 = -4 and 2 - 5 = -3 but -4 ÷ -3 = 4 ÷ 3
Want a bit more help with this before you begin? Why not watch this short video?
