Simultaneous equations can be solved by drawing the line representing each equation and then finding the point of intersection between the two lines.
Use y = mx + c, or other methods, to draw the lines.
Example
By drawing the lines of these equations on a set of coordinate axes, solve the following equations simultaneously:
y = x + 2
x + y = 3
Answer
y = x + 2 has a gradient of 1 and an intercept on the y-axis at (0, 2)
x + y = 3 can be rearranged to read
y = 3 - x which has a gradient of -1 and an intercept on the y-axis at (0, 3)
The lines are drawn on a set of coordinate axes.
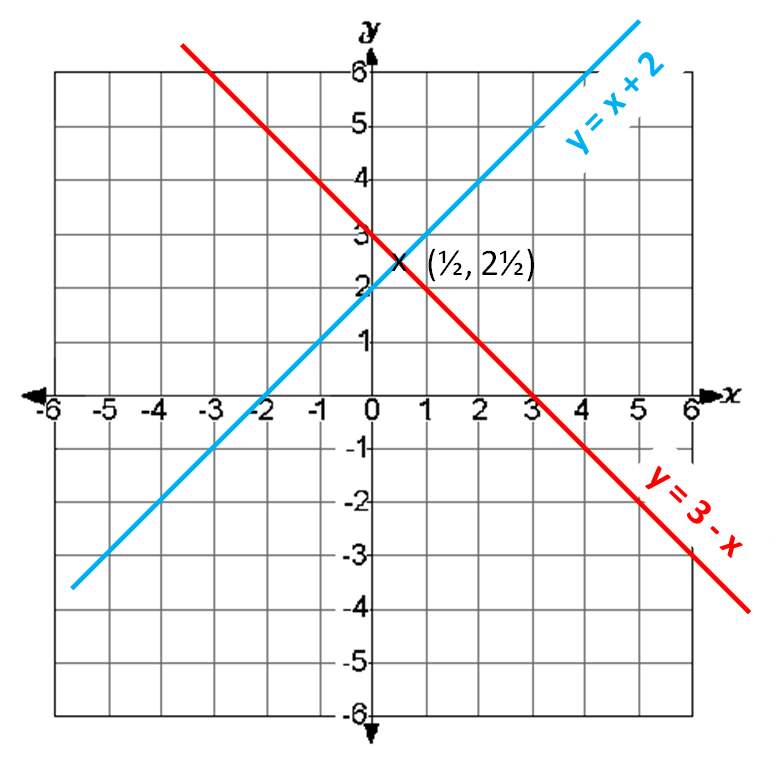
The point of intersection is (½, 2½) and this is the only point at which both equations are satisfied. We can also write this as (0.5, 2.5)
So the solution to the simultaneous equations is x = 0.5, y = 2.5








