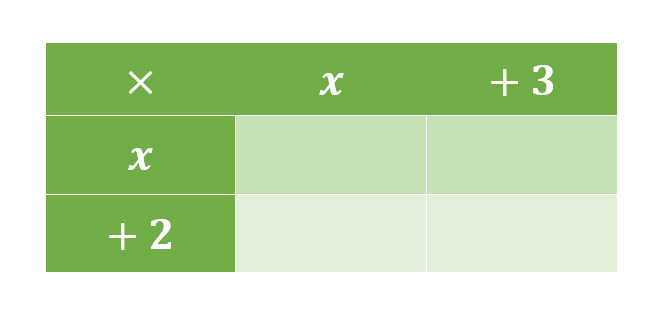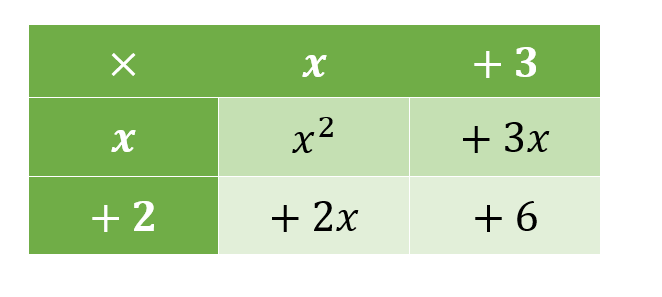Expand Products of Two Binomials

Expanding double brackets can be achieved using a variety of methods.

 

In this activity, we will focus on the grid method.

 

 

Let's take a look at an example.

 

e.g. Expand (x + 3)(x + 2).

 

First, we will set up a table like the one below:

See how the first bracket is on the top and the second bracket on the side?

 

Now we are going to multiply the first term on the left by both terms on the top row, then repeat with the second term on the left:

 

We need to make sure that our signs are correct here.

A positive number multiplied by another positive gives a positive outcome.

A negative number multiplied by another negative also gives a positive outcome.

But a negative number multiplied by a positive always gives a negative outcome. 

 

Now take all the terms we've just placed in a table and simplify as much as possible:

x² + 3x + 2x + 6 = x² + 5x + 6

 

So in summary, (x + 3)(x + 2) = x² + 5x + 6

 

 

 

In this activity, we will practise expanding double brackets using the grid method described above and then simplifying our answers. 

You may want to have a pen and paper to hand so that you can draw out your own grids.