A sequence is simply a set of numbers that follow a rule.
In this activity, we are going to look at linear sequences.
These are sequences that are increasing or decreasing by the same amount each time.
e.g. For the sequence 7, 9, 11, 13, ... give the next two terms and the rule.
We need to find the difference between each term in this sequence.
The terms are always separated by 2 and the numbers are increasing, so the rule is + 2.
Therefore, to calculate the next two terms, we simply need to apply this rule twice to the final number provided:
13 + 2 = 15
15 + 2 = 17
Let's try a visual example now.
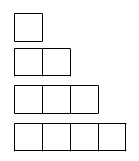
e.g. How many lines will be in the next diagram?
Whenever we have a question like this, where a sequence is drawn instead of given as numbers, our first step is to always turn it into a sequence which contains numbers.
If we count the lines in each diagram, we reach the following sequence:
4, 7, 10, 13, ...
So the rule is + 3 and the next diagram will have 16 lines.
You might also be asked to draw it, but we're sure you could do that if requested!
In this activity, we will find rules to describe both increasing and decreasing linear sequences (which increase/decrease by the same amount each time), and apply rules to find the next terms in sequences.
In this activity you should not use a calculator, but instead practise your mental calculations.