What are waveforms?
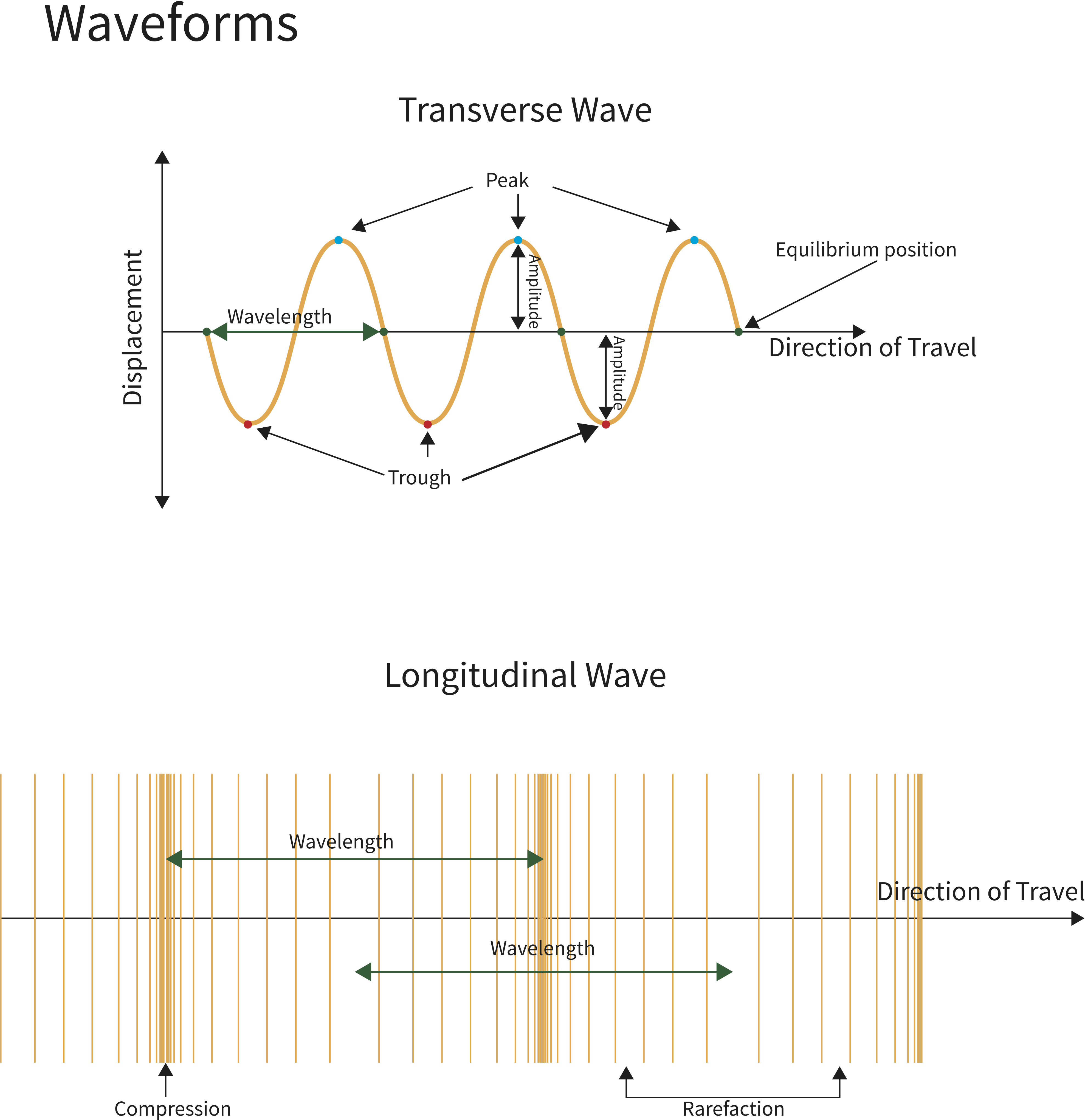
The diagram shows the characteristics of transverse and longitudinal waves. Light and water waves, although very different to each other, travel as transverse waves. In transverse waves, the vibrations are at a right angle to the direction of movement. The number of waves that pass through a certain point in one second is called the frequency of a wave.
The pictures below show water waves.

.jpg)
If you drop a stone or a water droplet on a smooth water surface, ripples will form, as shown in the photograph below.

Water is a transverse wave, as the direction of the vibrations and the direction of the wave are at right angles to each other (i.e. the ripples move up and down on the surface, while the wave itself travels side ways).
What is superposition?
When two waves occur in the same medium (the substance they travel in) at the same time, they interfere with each other and can combine. They can either add up or cancel each other out - a bit like addition and subtraction.
The principle of superposition is that when two or more waves meet at a point, the displacement at that point equals the sum of the displacements of each wave.
For example, if a wave with a displacement of 3 cm meets a wave with a displacement of 2 cm at a given point, then they make a new wave with a displacement of 5 cm at that point.
As we will see in the examples below, it isn't always as straightforward as just adding numbers together because displacements can be negative as well as positive. In these situations, you would have to subtract the displacements.
Constructive and destructive interference
Wave interference and superposition are shown in the diagrams below:
Each diagram shows the result of two waves combining, with the new wave shown at the top.
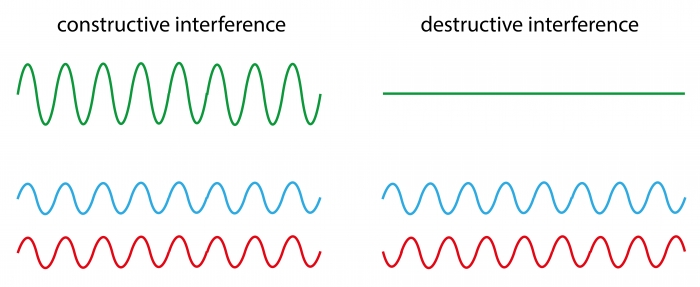
In constructive interference, the amplitudes of the two waves add up to form a new wave with a greater amplitude, shown by the green wave. Meanwhile, in destructive interference, we subtract the amplitudes of each wave, meaning the two waves cancel each other out, which is shown by the flat line.
Constructive interference occurs when the two waves line up with each other, while destructive interference happens when the two waves do not line up. Notice the peaks line up with each other for constructive interference (which is called being in phase), while in destructive interference, the peaks of one wave line up with the troughs of the other (which is called antiphase).
Despite wave interference, the waves themselves do not change and after the superposition - they will continue travelling as they were before, on the same path.
Lots to think about here, so remember that you can look back at this page at any point by clicking on the red help button on the screen.








