In this activity, you will be introduced to the wave equation, which will allow you to calculate a speed, wavelength, or frequency of a wave.
Frequency and wavelength
All waves have a frequency and a wavelength. Frequency is the number of waves per second and is measured in Hertz (Hz), while wavelength is the distance between two peaks, measured in metres.

Now, imagine a wave that is travelling at a constant speed, such as a wave on an oscilloscope screen.
What would happen to the wavelength if the frequency increased? Let's take a look at the effect.
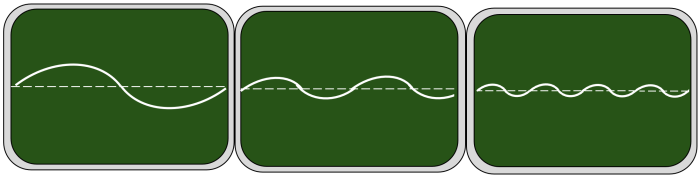
From left to right, the three different waves have been produced by increasing the frequency.
You will notice that the wavelength has decreased, and this makes sense. Producing more waves every second will 'squash' the wave into a smaller space, resulting in peaks that are closer together.
If we now examine closer and put some measurements into this, we will start to realise there is a mathematical relationship between frequency and wavelength:
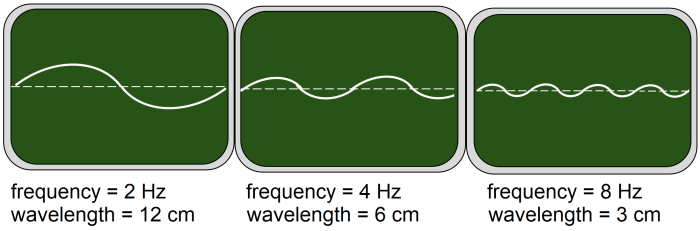
In this case, doubling the frequency halved the wavelength.
Furthermore, we then multiplied the original frequency by 4 and the original wavelength divided by 4.
So if we multiply one quantity by a given value, the other quantity divides by that same value.
Also notice that multiplying the pairs of values together gives the same answer each time (2 x 12, 4 x 6, and 8 x 3 all make 24). This is called inverse proportion.
The wave equation
As we have just seen, frequency and wavelength are inversely proportional for a wave with a constant speed. The equation that relates these quantities is as follows:
Speed (m/s) = Frequency (Hz) x Wavelength (m)
In symbols, it is: v = f λ
where v = velocity (speed), f = frequency, and λ = wavelength. (λ is a letter of the Greek alphabet called 'lambda').
So, you can calculate the speed of a wave by multiplying the frequency and wavelength together.
The equation can also be rearranged to find frequency or wavelength:
f = v ÷ λ
λ = v ÷ f
So, as long as you use the equation in the correct arrangement, you will always be able to calculate a speed, wavelength, or frequency of a wave.
Just make sure that frequency is in Hertz and wavelength is in metres, otherwise your units will not produce a speed in metres per second.
Now that you have seen the equation, have a go at using it in the upcoming questions.







