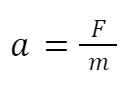Apply Newton's Second Law to Solve Calculations

Isaac Newton wrote the three laws of motion, helping us to understand how forces affect objects and their movement. In this activity, we will be looking at how we can use Newton's Second Law in calculations.

 

 

Described in words, Newton's Second Law states that a resultant (or unbalanced) force on an object can make that object change its speed or direction. 

It also says that the size of the force affects how quickly the motion of the object changes. 

Let's look at this in more detail. 

 

Acceleration can be defined as the rate of change of speed. In other words, the greater the acceleration, the more an object speeds up per second. 

The unit acceleration is measured in is m/s². This is a bit of a tricky unit, we need to try not to mix it up with the unit for speed, which is m/s.

 

If a dog has an acceleration of 1 m/s², that means the dog gets faster by 1 m/s, every second.

 

 

Imagine a cyclist travelling along a path. If they increase the force they apply to the pedals, they accelerate. What this means is that the speed of the cyclist will increase every second.

 

What if the cyclist used an even greater force on the pedals? That would cause a greater acceleration! What that would mean is that the cyclist increases their speed every second, even faster than before. 

 

What if the cyclist had to carry a very heavy parcel in their bike storage? The increased mass would make it harder for the force to speed up the bike. The greater the mass, the lower the acceleration. 

 

 

What this means is that we can express Newton's Second Law as an equation:

 

 

Or, using symbols to make things a little simpler:

 

 

Example 

A person runs with a forward resultant force of 140 Newtons. They have a mass of 70 kg. 

What is their acceleration?

 

 

Answer 

First, let's write down the equation. 

 

 

Acceleration (m/s²) = 140 N ÷ 70 kg = 2 m/s²

 

So, every second, this runner gets 2 m/s faster. 

 

Example 

A hamster has a mass of 200 g. It runs forwards with a force of 1.5 Newtons. What is the acceleration of the hamster?

 

 

Answer 

There is a step we need to follow before we use the equation - we have to convert the mass to kg! Otherwise, the equation won't work. 

To convert, we need to divide by 1,000.

200 ÷ 1,000 = 0.2 kg

 

 

a (m/s²) = 1.5 ÷ 0.2

a (m/s²) = 7.5 m/s²

 

 

Now let's practise applying what we have learnt!