EdPlace's Year 7 home learning maths lesson: Finding the Nth Term

Looking for short lessons to keep your child engaged and learning? Our experienced team of teachers have created English, maths and science lessons for the home, so your child can learn no matter where they are. And, as all activities are self-marked, you really can encourage your child to be an independent learner.

Get them started on the lesson below and then jump into our teacher-created activities to practice what they've learnt. We've recommended five to ensure they feel secure in their knowledge - 5-a-day helps keeps the learning loss at bay (or so we think!).

Are they keen to start practising straight away? Head to the bottom of the page to find the activities.

Now...onto the lesson!

Key Stage 3 Statutory Requirements for Maths

Year 7 students should be able to recognise arithmetic sequences and find the nth term.

What's It All About?

Sequences are a common topic in Key Stage 3 and having a good understanding will be a useful skill. Most students can work out missing numbers in lists or work out a term-to-term rule, but students need to also be able to understand the algebra behind a sequence. This will allow them to examine a sequence in more depth and arrive at answers much faster. We're confident that if you follow this step-by-step approach together, your child will be able to:

1) Interpret an arithmetic sequence

2) Derive an expression for the nth term

3) Apply the expression to find given terms in a sequence

Where to Start?

The first thing to do with your child is to define an arithmetic sequence. Quite simply, it's a sequence that changes by the same amount each time. The word term simply refers to the number in the sequence, for example, these sequences have a first term (the first number), a second term (the second number), a third term (the third number), etc. The idea of having an expression for the “nth” term is that you can use it to work out any term in the sequence.

Arithmetic Sequence

In the following steps, we will learn how to find the nth term of arithmetic sequences.

Step 1 - What's Meant by the Nth Term?

Nth Tern

If we want to find the nth term of this sequence, the first thing we need to do is work out the progression (in other words, how the sequence progresses from one term to the next). We simply write the progression as a number, then put “n” after it.

We know that this sequence increases by 2 each time, so the first thing we do is write 2n.

Step 2 - Putting the Nth Term Back into the Sequence

All we then need to do is consider the sequence we would generate with the expression we have just written. Think of it this way: 2n means the 2 times table; 3n means the 3 times table; and so on.

In our example of 2n, the sequence would be 2, 4, 6, 8, … We just have to compare this to the sequence we have:

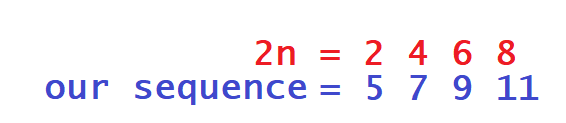
Nth Term 2

We can see that every term in 2n just needs to have 3 added in order to become our sequence, so we add this on to the end of our expression and there we have it!
The nth term of the sequence is 2n + 3.

Step 3 - What Are the Benefits?

So, finding the nth term is really as simple as seeing how much the sequence changes by, then comparing it to the relevant times table. Let us now look at how we can use this to work out any given term. If you have an expression for the nth term and want any given term number, you just have to substitute your term number for “n”.

For example, we know the nth term of our sequence is 2n + 3.

If we want the first term, we make n = 1. (2 x 1 + 3 = 5).

If we want the second term, we make n = 2. (2 x 2 + 3 = 7)

If we want the 1000th term, we make n = 1000. (2 x 1000 + 3 = 2003)

And so on...

So if your child was ever faced with an exam question that gave them a sequence and asked them for the 1000th term, the great news is they don’t need to write out 1000 numbers to get there: they can just use the expression for the nth term and plugin 1000.

Step 4 - Putting it into Practice

One last thing you and your child may want to do with an nth term expression before setting them off on their own is to use it to prove or disprove whether a number occurs in a sequence.

For example: In 2n + 3, will the number 564 occur?

We could sit down and write out the entire sequence 5, 7, 9, 11… until we reach the 560s, but there's no need! This is what to do:

Make the nth term EQUAL the number you are interested in.

2n + 3 = 564

This has turned it into an equation. SOLVE for n:

2n + 3 = 564

2n = 561

n = 280.5

If your final answer of “n” is a whole number, the number is in the sequence. If it's not a whole number (as in our example), the number is not in the sequence.

That makes sense if we think about it – we have found that n = 280.5; you can have the 280th term of a sequence and a 281st term, but you can’t have a 280.5th term. See? Lot's of ways we can use nth terms to make things much quicker! Once you've looked at this why not see if you can do the following questions together?

1) Is 3, 6, 9, 15, 24 … an arithmetic sequence? Explain your answer.

2) Find the nth term of 7, 12, 17, 22, 27…

3) Find the nth term of 3, -1, - 5, - 9…

4) A sequence has the nth term 8n – 6. What is the 50th term of the sequence?

5) Does 543 occur in the sequence 5n + 3? Show your working.

Step 5 - Give it a go...

Why not test your child's understanding and see if they can tackle these activities?

All activities are created by teachers and automatically marked. Plus, with an EdPlace subscription, we can automatically progress your child at a level that's right for them. Sending you progress reports along the way so you can track and measure progress, together - brilliant!

Activity 1 - Write the First Five Terms of a Sequence from a Given Rule

Activity 2 - Understand Common Integer Sequences

Activity 3 - Arithmetic Sequences (the Nth Term)

Activity 4 - Write the Terms of a Sequence from a Formula

Activity 5 - Mixed Sequences

Answers

1) It is not arithmetic because the terms do not change by the same amount each time.

2) 5n + 2

3) -4n + 7

4) 8n – 6 where n = 50:

(8 x 50) – 6 = 394

(5) 5n + 3 = 543