Practise Subtracting Numbers With More Than Four Digits

In this activity, we are going to practise subtracting numbers with more than four digits.

The column method is an efficient method for subtracting large numbers, so this is what we are going to use.

We will be exchanging/carrying in some questions - sometimes more than once!

Top Tips:

Write each question out clearly - it can be useful to use squared paper if you are writing out the questions.

Check the digits are in the correct order (it is easy to muddle them up!)

Make sure each digit is in the correct column.

Start at the ones and work towards the left-hand column.

We could use the inverse operation to check our answers! 

We can't do subtraction in any order like we can with addition.  (3 - 8 can not be written as 8 - 3)

Example

Subtract the following 

64,576 - 42,443

We set out the question as shown in the example above.

Each digit must go in the correct column as shown.

Next, we subtract the bottom number from the top starting with the ones.

The ones: 6 - 3 = 3  We put the 3 in the ones column.

The tens: 7 - 4 = 3  (70 - 40 = 30)

The hundreds:  5 - 4 = 1 (500 - 400 = 100)

The thousands: 4 - 2 =  2 (4,000 - 2,000 = 2,000)

The ten thousands: 6 - 4 = 2 (60,000 - 40,000 = 20,000)

The answer is 22,133

There was no exchanging/carrying in this question.

Now let's have a look at a question where we need to exchange.

 Subtract 33,825 from 75,468 

We set out the question as shown in the example above.

Each digit must go in the correct column as shown.

We then subtract the bottom number from the top starting with the ones column.

The ones: 8 - 5 = 3  We put the 3 in the ones column.

The tens: 6 - 2 = 4  (60 - 20 = 40)

The hundreds: 4 - 8 =  (400 - 800)  We can't do this, so need to exchange 1,000 and put it into the hundreds column.

14 - 8 = 6 (1,400 - 800 = 600)

The thousands: we now have 4 - 3 in this column, 4 - 3 = 1 (4,000 - 3,000 = 1,000)

The ten thousands: 7 - 3 = 4 ( 70,000 - 30,000 = 40,000)

The answer is  41, 643

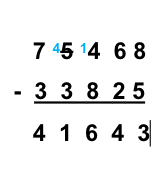
Now why don't we have a go at answering some questions?

Remember, we can do the inverse (opposite) operation to check answers!

We can come back and look at the examples if we need to by clicking on the red help button on the screen.