Recognise Straight Line Graphs

In this activity, we will be looking at how sequences link to straight line graphs.

 

Let's take the sequence:

2, 4, 6, 8 ,10, .........

We can see that this is the 2 times table, so the rule for this is 2n

 

What about 

3, 5, 7, 9, 11, ........

This still goes up in 2's so the rule is 2n, but each term is not 2, 4, 6 etc

Each term is 1 more than the 2 times table.

Therefore, our rule for this one is 2n + 1

 

 

We can apply this rule to recognising and drawing straight line graphs.

We use y and x, but it is just a sequence of coordinates which join to form a straight line.

 

See the graph of y = 2x + 1 below:

 

 

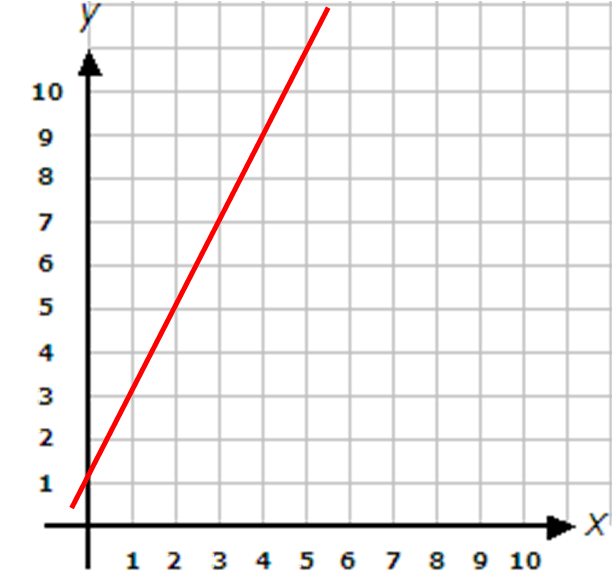
As in the sequence, the line starts at y = 1 and goes up in 2's (that is 1 across, 2 up)

 

We can recognise a straight line graph because it goes up or down by a constant value (2 in this case).

If the x was x² or x³ etc it would not be constant, so would form a curve.

 

Let's look at a typical question!

 

Example

Which of the equations below form a straight line graph?

y = 3x - 5                                y = 2x + x²

 

Answer

y = 3x - 5 is the answer as it goes up by 3, which is constant.

The x² term in the other equation makes the graph form a curve.

 

Let's have a go at some questions!