Find Side Lengths and Angles in Right-angled Triangles

In a right-angled triangle, the sides and the angles are connected by three trigonometric ratios.

 

 

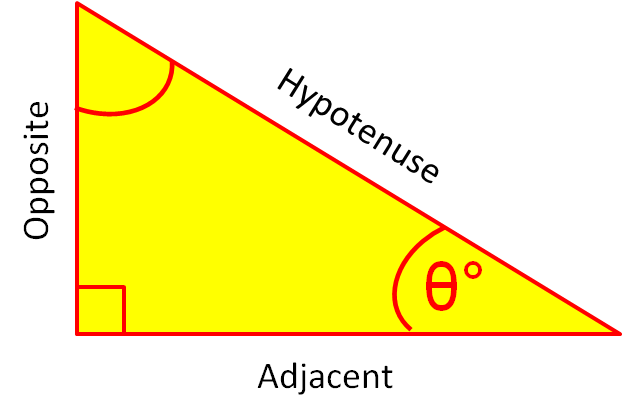
The three trig ratios are:

 

 

The best way to use these is in a formula triangle:

 

For example with sin:

 

 

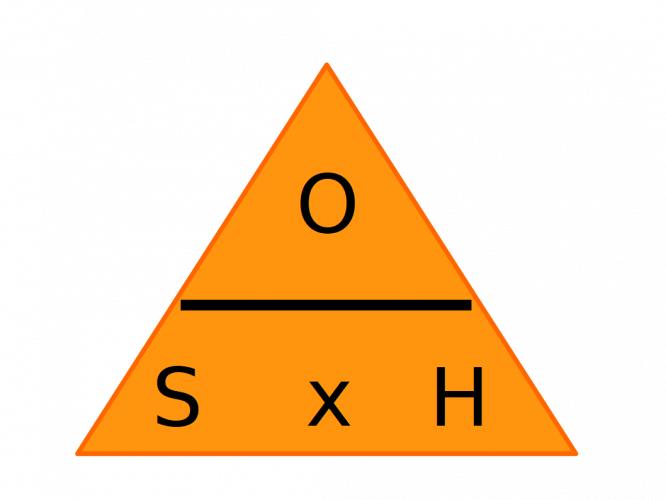
The triangle above shows the formula triangle for using sin. 

To use it, we simply cover up the part of the triangle that we want to find out and then rearrange the equation.

 

For example, if we know the sin and the opposite side, we cover up H (the hypotenuse) and we can see that we need to do: O ÷ S = H see below

 

 

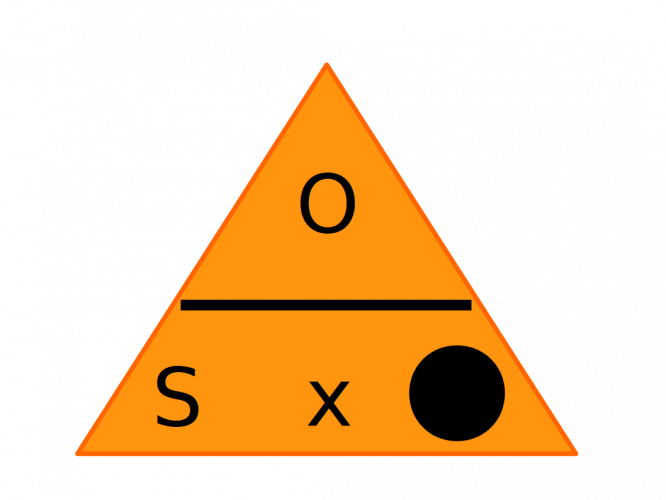
If we know the sin and the hypotenuse, we cover up O and we can do this equation: S x H = O see below:

 

 

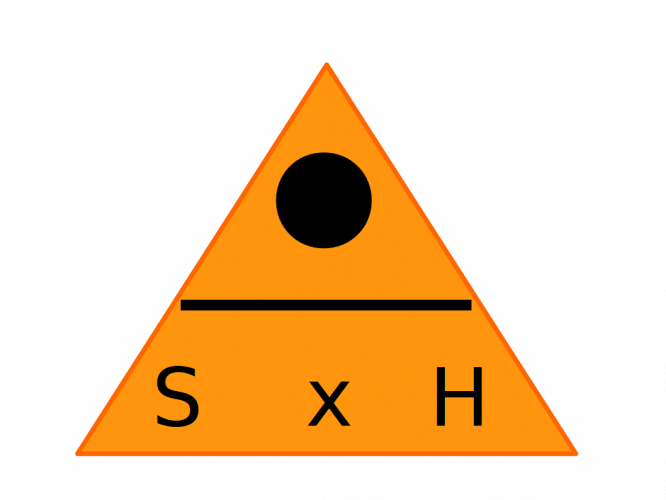
Clearly, if we know O and A but don't know S, we'd cover up S and do O ÷ H = S

 

We can remember the triangle by using the letters SOH to spell a sort of word!

 

We can do the same for the other two formulae too:

 

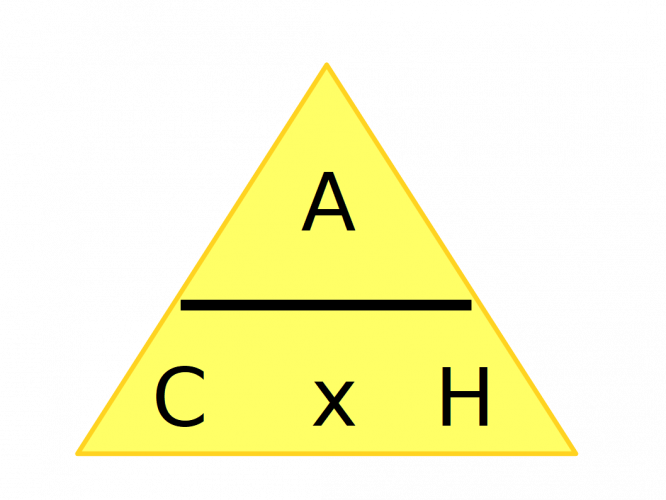
Here is the triangle for cos - we can remember this one by the word CAH

 

 

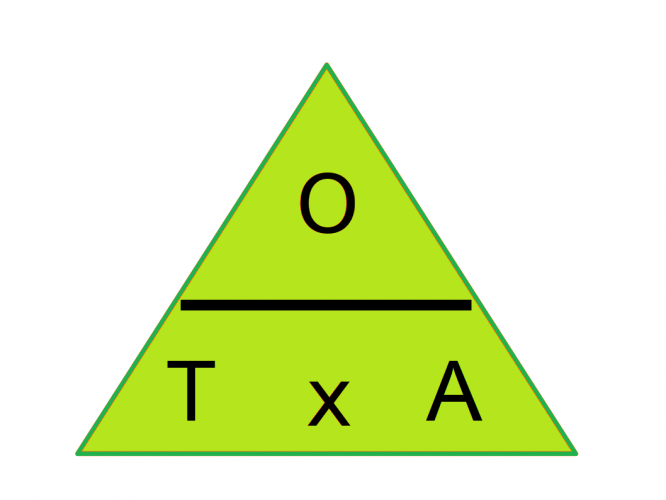
And here's the one for tan - we can remember this one by the word TOA

 

 

We can stick the words together to make a pretty silly-looking word:

 

SOHCAHTOA 

 

Example 1

Using trigonometry, calculate the side length x to 3 sig. figs.

 

 

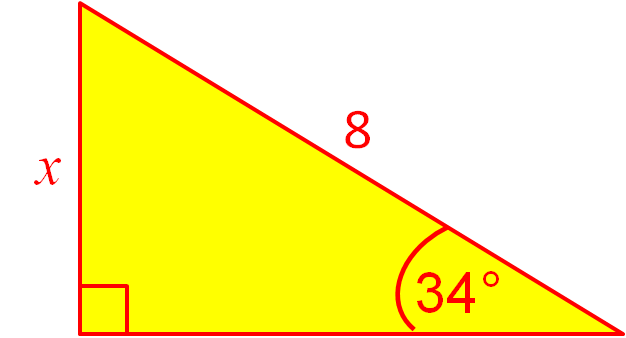
Answer

Label the sides adjacent, opposite and hypotenuse in relation to the given angle 34º.

The given sides are the opposite (x) and the hypotenuse (8). We don't need to know the adjacent side.

 

So, we know the hypotenuse and the angle, and we need to find out the opposite side. So which formula do we need that has S, O and H in it?

It's the SOH one with SIN!

 

 

Which letter do we need to cover up in the triangle? The side we want to find out is O, so cover up O and we do H x Sin

 

x = 8 sin34º

x = 8 x  0.559192903....

x = 4.47 (3 s.f.)

 

Example 2

Using trigonometry, calculate the angle θº to 3 sig. figs.

 

 

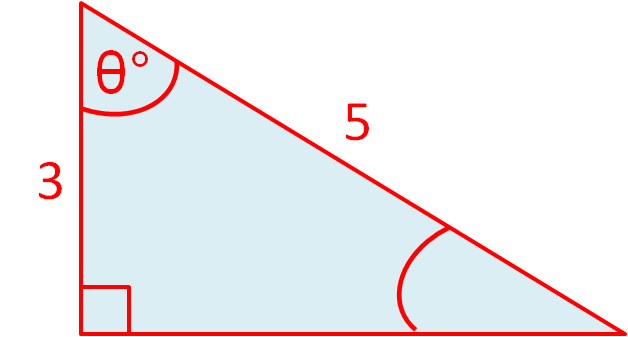
Answer

Label the sides adjacent, opposite and hypotenuse in relation to the angle θº.

The given sides are the adjacent and the hypotenuse.

 

Which formula do we need that includes the angle, adjacent and hypotenuse? It is CAH

 

 

 

We know the adjacent and the hypotenuse, so in the formula triangle, we need to cover up C.

 

This gives us:

 cos angle = adjacent ÷ hypotenuse

 

cos θ = 3 ÷ 5 = 0.6

 

To find the angle itself, we need to do the inverse of cos.

First, make sure that your calculator is in degrees mode.

 

θ = cos^-1 0.6

θ = 53.1º (3 s.f.)

 

Let's have a go at some questions.