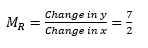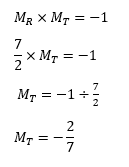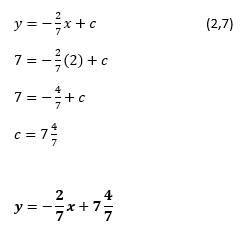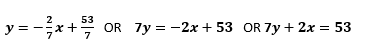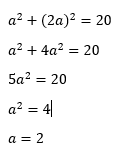At GCSE level, examiners frequently like to put two or more topics together in a question as this allows them to test problem-solving.
At higher level, you are likely to see a question that ties together the equation of a circle, the equation of a straight line, circle theorems and perpendicular lines. (Phew!)
Luckily, if you ever come across this question, the method you need to use to solve it is always the same.
Example:
A circle has the equation x2 + y2 = 53
Find the equation of the tangent to the circle at the point (2,7)
Step 1: Sketch the situation. If you sketch the shape, you are much less likely to make a mistake with the gradient and intercept of the tangent.
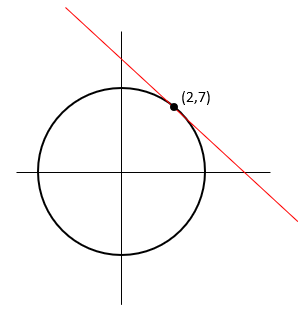
Straight away, there are a couple of things we can put on this diagram.
If we draw a line from the centre to the point, we are drawing a radius.
We can then say (because of circle theorems) that the radius and the tangent meet at 90°.
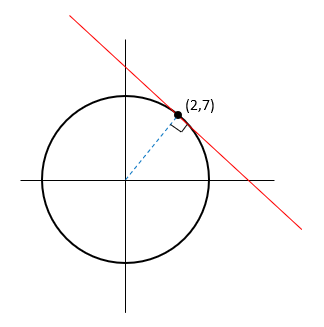
Step 2: Find the gradient of the radius.
We know that the radius at this point will be found by using:
Step 3: Use the gradient of the radius to find the gradient of the tangent.
Because these two lines meet at 90°, we can say that their gradients multiply to make -1.
Step 4: Use the gradient and the point (2,7) to find the equation of the tangent.
If you’re not sure about this step, why not have a look at the activity on finding the equation of a line.
Remember that this could also be written as:
They all mean exactly the same thing!
The extension.
While it’s common to see this topic laid out exactly as it is above, the exam boards have been known to throw an extension in where the point is given algebraically instead of giving the coordinates.
Example:
A circle has the equation x2 + y2 = 20
Find the equation of the tangent to the circle at the point (a,2a)
The only difference here is that our first step is to find the coordinates of the point first.
We know that the point (a,2a) lies on the circle, so it must therefore satisfy the equation of the circle.
From this, we can find that the point on the circle we are dealing with is (2,4)
Let's try some questions now.