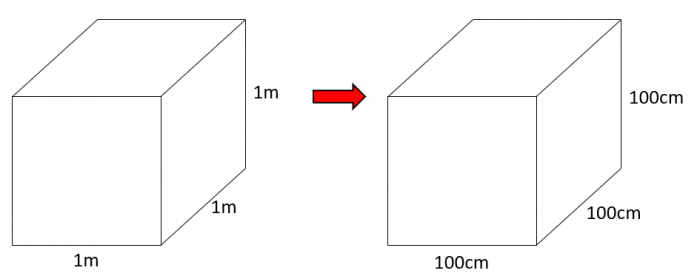
Converting volume units of measurement can be a challenging concept, as we need to ensure we consider volume conversion factors.
When we are converting from, for example, metres into centimetres, we know that 1 m = 100 cm.
This leads to the misconception that 1 m3 = 100 cm3.
BUT, in reality, 1 m3 = 1,000,000 cm3.
Let's look at what's happening here with a diagram to help.
Looking at the volume of these two identical cubes, we can say that:
1 m × 1 m × 1 m = 100 cm × 100 cm × 100 cm
1 m3 = 1,000,000 cm3
Is there a trick here?
In a way, yes.
All we need to do for a volume conversion is to find the conversion if we were dealing with a length and then cube it to get the volume conversion factor.
Let's look at this process in action with some examples now.
e.g. Convert 1.4 m3 into cm3.
We know that for length, 1 m = 100 cm.
So for volume, 1 m3 = 1,000,000 cm3.
So 1.4 m3 = 1.4 × 1000000 = 14000000 cm3.
e.g. Convert 350 m3 into km3.
We know that for length, 1 km = 1000 m.
So for volume, 1 km3 = 1,000,000,000 m3.
So 350 m3 = 350 ÷ 1000000000 = 0.00000035 m3.
In this activity, we will convert volume amounts between different units of measurements (cm3, m3, km3) using the method shown above of calculating and applying a volume conversion factor.