Standing on a bridge with a river running underneath, the person to your left asks you to step off the scales and puts some numbers into a computer. They look at you and smile as they ask you ‘How much do you want to go into the water?’ You look scared, adrenaline running through your body as you say, ‘About up to my waist?’. They play with some numbers on the screen and then ask you if you are ready. You slowly nod and they start a countdown ‘3, 2, 1’. With a slight hop, you are in the air, plummeting towards the water headfirst – it feels like forever, but in only a few seconds, you feel the bungee cord pulling at your legs, slowing you down as your body dips into the water up to your waist and you get pulled back up. Bungee jump, done! It takes a lot of maths to be an expert thrill seeker - you need to know where the limits are, so you don’t die. In this activity, we'll be looking at some of the science that allows us to perform bungee jumps – Hooke’s law and elastic forces.
A bungee cord is basically a big rubber band, and it might help some of this to sink in if you have a rubber band to play with while you read this. If you apply just one force to a rubber band then it won't stretch, it will just move in the direction the force is applied. You need a minimum of two forces that will act in different directions to stretch anything. One of these forces could be stationary, such as your finger, and one could be moving, like your hand pulling the band backwards. This will apply a force to the band and make it stretch. If you release the forces, the band will return to its original shape. All good so far?
Okay, so Hooke’s law is a law that defines stretching things. It says that ‘the force applied to an object is proportional to the length of the extension’. This basically means that if you were to plot force and extension on a graph, it would make a straight line.
Hooke realized that he could make an equation out of this graph that could tell him, in any given circumstance, what the extension of an object would be.
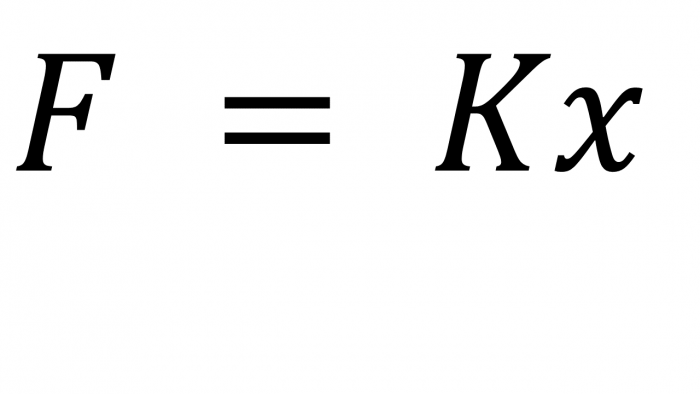
F = force (newtons (N))
k = spring constant – a number that tells you how hard it is to stretch the object (newtons per metre (N/m))
x = extension – how much the spring has stretched (metres (m)) This is often also written as e for extension and this is what we will be using in this activity.
So, the person putting the numbers into the computer at the start of the activity was just working out how much you would stretch the bungee, using this equation.
Let’s have a go at this ourselves.
Question: A person stretches the bungee 15 m when the bungee cord has a spring constant of 40 N/m. Calculate the force applied by that person.
Step 1 Highlight the numbers in the question:
A person stretches the bungee 15 m when the bungee cord has a spring constant of 40 N/m. Calculate the force applied by that person.
Step 2 Write out the numbers:
F = ?
k = 40 N/m
e = 15 m
Step 3 Put the numbers into the equation:
F = 40 x 15
Step 4 Do the calculation and write out your answer:
F = 600 N
Don’t forget your units!
Let's have a go at some questions now.