
EdPlace's KS3 home learning maths lesson: Using the Term to Term Rule in a Sequence
Looking for short lessons to keep your child engaged and learning? Our experienced team of teachers have created English, maths and science lessons for the home, so your child can learn no matter where they are. And, as all activities are self-marked, you really can encourage your child to be an independent learner.
Get them started on the lesson below and then jump into our teacher-created activities to practice what they've learnt. We've recommended five to ensure they feel secure in their knowledge - 5-a-day helps keeps the learning loss at bay (or so we think!).
Are they keen to start practising straight away? Head to the bottom of the page to find the activities.
Now...onto the lesson!
Sequence... What Comes Next?
Sequences occur frequently in everyday life and we’re used to spotting the rules of a sequence without even worrying about it – for example finding a house number 10 in a street. But, can you find the next number in this sequence and explain the term to term rule you have used? If you're not sure what the pattern is in the following sequence, don't worry! 1 3, 6. 10, 15 … (We'll come back to this later!)
We're confident that if you follow the step-by-step approach below your child will be able to:
1) Understand how to generate a sequence from the term to term rule
2) Apply this knowledge to solve the sequences
3) Explain their reasoning clearly
Step 1 - Terrified of the Terminology?
Before we jump into adding fractions with different denominators it’s important to check that your child understands what the key terminology means.
A sequence is a collection of objects (in most mathematical cases it’s a collection of numbers) that are in order and follow a particular rule. For example, the odd numbers (1,3,5,7,9…) are a sequence. Each individual number in a sequence is a term in the sequence, and we'll need to find the operation, such as adding or subtracting a number that will allow us to work out the next number in the sequence. This rule is known as the term-to-term rule.
Step 2 - Checking Prior Knowledge
So, where do we start when trying to work out the sequence? We need to be able to find the differences between 2 numbers or to work out whether the next number can be found by multiplying or dividing the previous number. Why not practice a few quick subtraction questions or a few times table questions?
Step 3 - Next Up Is...
Here’s a simple example of finding and using a term to term rule to find the next term in this sequence.
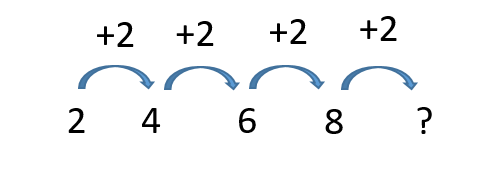
We can see that the difference between the 1st and 2nd terms of the sequence (2 and 4) is 2, and we can also add 2 to move from the 2nd to the 3rd, and so we can find the 5th term in the sequence by using the term to term rule of adding 2 to the 4th term (8) and so the correct answer is 10.
This is a descending sequence, where the next term is smaller than the previous term.
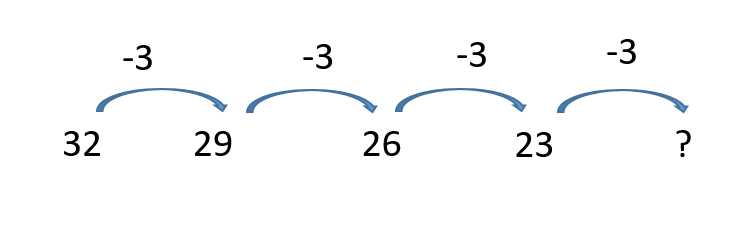
We move from term to term by subtracting 3, and so the next 2 terms in this sequence would be 20 and 17. The numbers in this sequence will eventually become negative. Can you work out what the first negative number in this sequence would be? Both of these sequences are examples of arithmetic or linear sequences because the term to term rule involves adding or subtracting a constant amount.
A geometric sequence has a term to term rule that involves multiplying (or dividing) by a number

This sequence again starts with 2 and 4, but we can see by looking at the 3rd term that we aren’t adding 2 to each term, but we are multiplying the previous term by 2 to find the next term. So, 16 x 2 = 32, and the next term is 32. Do you think that the number 99 will be in the sequence? As 99 is an odd number and multiplying by 2 only produces even numbers, the answer has to be no. Can you explain why 100 won’t be in this sequence? (Hint, think about the factors of the numbers that are in the sequence.)
Some sequences are based on square numbers, and these are called quadratic sequences
The square number sequence starts 1, 4, 9, 16, 25 because
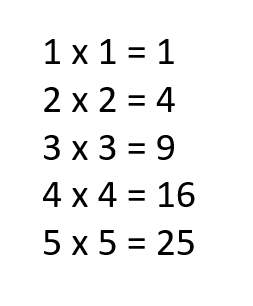
So, the next term would be 6 x 6 = 36. Trying exploring the differences between these numbers- what do we need to add to move between the terms? Are there any patterns to the gaps?
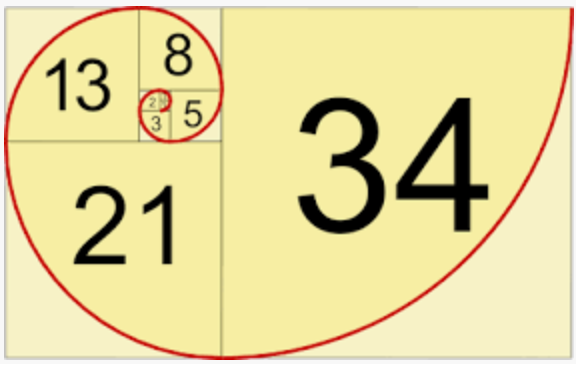
Another type of sequence can be made by adding previous terms together. Here is an example. We start with 0 and 1 and add these first 2 terms together to get the 3rd term which is also 1. The 4th term is the 2nd + 3rd term which is 1 + 2 = 3 and so on. This gives us 0,1,1, 2, 3, 5, 8, 13, 21….
This type of sequence is called a Fibonacci sequence and they can be found in nature. Try looking at sunflower seeds and snail’s shells!
Step 4 - Who's Next In Line?
Now we can practice finding the term to term rule and the next term for all these different types of sequence.
1) 1, 4, 7, 10, …
2) 14, 10, 6, 2, …
3) 3, 9, 27, 81…
4) 125, 25, 5, 1 …
5) 2, 8, 18, 50, ... ( Hint- think of square numbers)
6) 1, 4, 5, 9, 14, …
And here’s a thinking question for each of the above sequences.
1) Is 99 in this sequence? Is there a quicker way to tell, rather than repeatedly adding 3?
2) What is the 50th term in this sequence? Why not think about how many times you need to subtract 4 from the starting number of 14?
3) What are the prime factors of all the numbers in this sequence?
4) Can you write the numbers in this sequence in index form?
5) Can you find any patterns with the differences between the numbers in this sequence? Are they different patterns to the numbers in the original square number sequence?
6) Find some more examples of Fibonacci sequences in nature or architecture.
Step 5 - Give it a go...
Now, you’ve covered this together why not put this to the test and assign your child the following 5 activities in this order.
All activities are created by teachers and automatically marked. Plus, with an EdPlace subscription, we can automatically progress your child at a level that's right for them. Sending you progress reports along the way so you can track and measure progress, together - brilliant!
Activity 1 - Understand Common Integer Sequences
Activity 2 - Write the First Five Terms of a Sequence from a Given Rule
Activity 3 - Arithmetic Sequences
Activity 4 - Fibonacci Sequences
Activity 5 - Geometric Sequences
1) Rule = add 3, next term 13
2) Rule = subtract 4, next term -2
3) Rule = multiply by 3, next term 243
4) Rule = divide by 5, next term 0.2
5) Rule = 2 x next square number , next term = 2 x 36 = 72
6) Rule = add the 2 previous terms , next term = 23
Keep going! Looking for more activities, different subjects or year groups?
Click the button below to view the EdPlace English, maths, science and 11+ activity library









