In this activity, you will need to find missing angles.
Missing angles on a straight line
Angles on a straight line add up to 180°
To calculate a missing angle on a straight line, take away the known angle from 180°
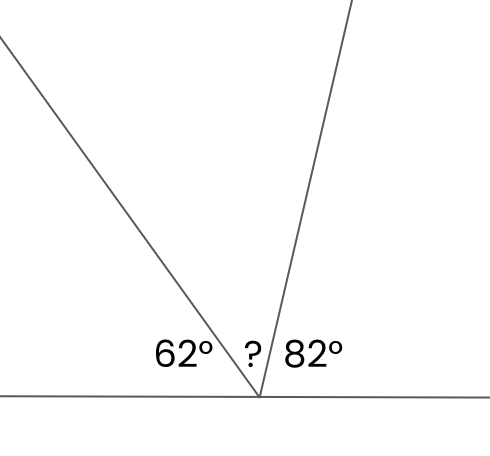
Here we have 62 and 82. If we add these together we get 144.
To find the missing angle we do 180 - 144 = 36
The missing angle is 36 degrees!
We could double check by making sure they all add up to 180 which they do!
62 + 36 + 82 = 180
Missing angles in a full turn
Angles in a full turn add up to 360°
To calculate a missing angle in a full turn, take away the known angle from 360°
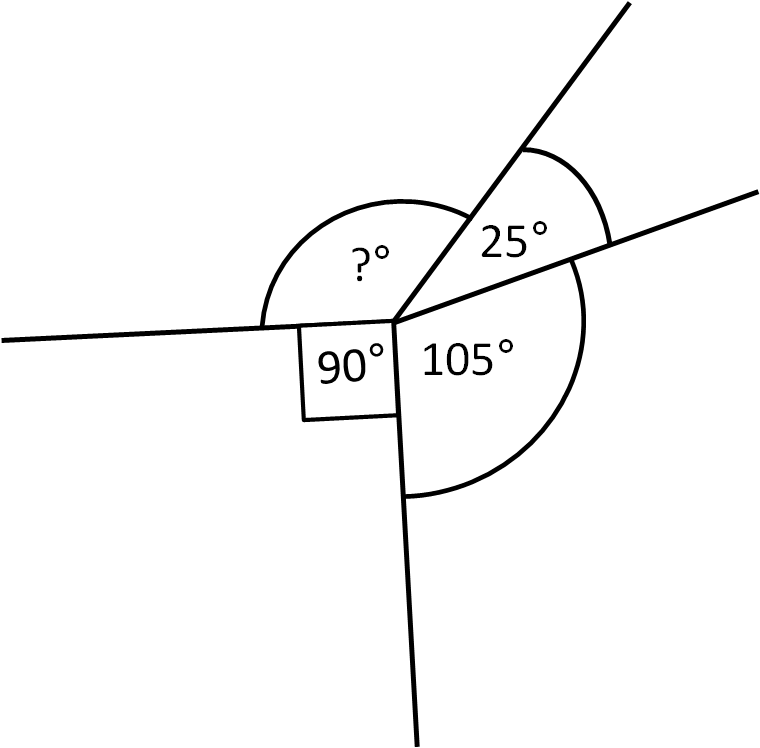
Here we already have 90 + 105 + 25 = 220
To find the missing angle we subtract these from 360.
360 - 220 = 140
So the missing angle is 140 degrees.
Let's check: 90 + 105 + 25 + 140 = 360!
Missing angles on intersecting lines
All four angles will add up to 360°
Opposite angles on a cross are equal.

So here, if we know that one angle is 15 degrees, we know the opposite angle on the cross, marked here with a question mark, will also be 15 degrees.
Missing angles in quadrilaterals
A quadrilateral is any shape with four sides.
For example: square, rhombus, trapezium, parallelogram.
The angles in a quadrilateral add up to to 360°

I think you've got the right angle on this now. Let's have a go at some questions.








