Understand and Calculate Missing Angles Using Known Angle Facts

Fantastic effort! You have decided to spend some valuable time practising for your maths SATs test.

 

In this activity, we will look at how to find the missing angle in a shape or around a point.

 

How do we find missing angles on a straight line?

 

The angles on a straight line add up to 180°.

To calculate the missing angle on a straight line, take away the known angle from 180°.

 

 

180° - 65° = 115°

 

How do we find missing angles in a full turn?

 

The angles in a full turn up add up to 360°.

To calculate the missing angle in a full turn, take away the known angle from 360°.

 

 

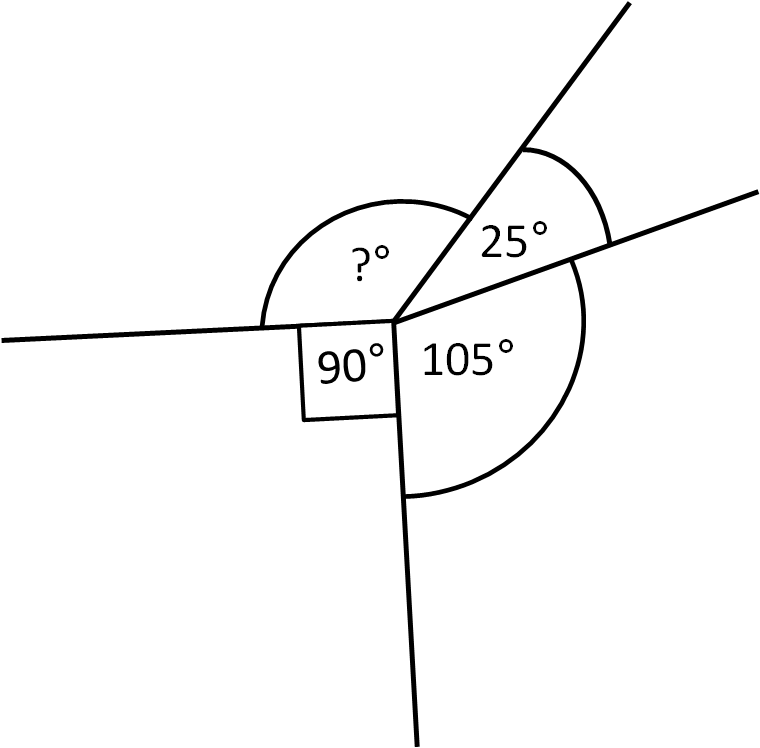
105° + 90° + 25° = 220°

360° - 220° = 140°

 

How do we find missing angles on intersecting lines?

 

All four angles will add up to 360°.

Opposite angles on a cross are equal.

 

 

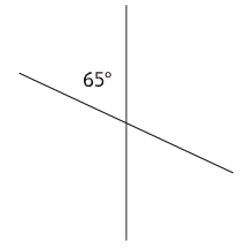
Step 1 (we know the angle opposite 65° is also worth 65° so add these together): 65° + 65° =130°

Step 2 (subtract the total of these two angles from 360°): 360° - 130° = 230°.

Step 3 (Divide this total by 2 to find what each of the two remaining angles is worth): 230°÷ 2 =115°

 

How do we find missing angles in a triangle?

 

The angles in a triangle always add up to 180°.

To find the missing angle, add together the known angles and subtract from 180°.

 

 

If you are given a triangle like this, but asked to find the missing angle, focus only on the angles given, ignore the other information.

 

57° + 90° = 147°

180° - 147° = 33°

 

How do we find missing angles in a quadrilateral?

 

A quadrilateral is a shape with four straight sides, like a square, rhombus, parallelogram, trapezium, rectangle.

The angles in a quadrilateral will add always add up to 360°

To find the missing angle, add together the known angles and then subtract from 360°

                                                     

 

90° + 90° + 40° = 220°

360° - 220° = 140

 

Now we have revised those key facts, time to have a go at some practice questions!

 

Good luck!