In this activity, we will divide numbers with up to four digits by two-digit numbers using long division.
There will be remainders which can be left as simple remainders.
Long division is similar to short division, but more of the working is shown on paper.
Let's look at 1989 ÷ 15
Short Division
First, we remind ourselves of how this would be worked out using short division.
We set out the calculation like this and then start dividing.
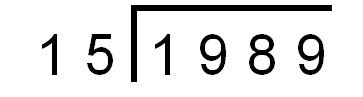
First, we divide 19 ÷ 15 = 1 rem 4.
(Remember that 1 × 15 = 15 and so the remainder is 19 - 15 = 4.)
The 4 goes next to the 8 to form 48.
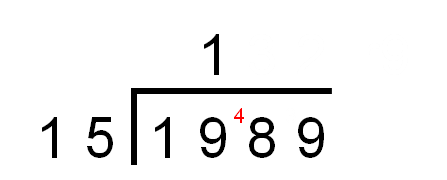
Then, we divide 48 ÷ 15 = 3 rem 3.
(Remember that 3 × 15 = 45 and so the remainder is 48 - 45 = 3.)
The 3 goes next to the 9 to form 39.
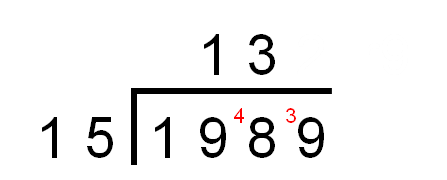
Lastly, we divide 39 ÷ 15 = 2 rem 9.
(Remember that 2 × 15 = 30 and so the remainder is 39 - 30 = 9.)
.png)
We have shown that 1989 ÷ 15 = 132 r9

Long Division
Now we will look at the same division worked out using long division.
We start by setting out the calculation in the same way, like this, and then start dividing.
First, we divide 19 ÷ 15 = 1 rem 4.
(Remember that 1 × 15 = 15 and so the remainder is 19 - 15 = 4.)
In long division we actually set out the subtraction under the 19.
.png)
In short division we put the 4 next to the 8 to form 48.
In long division, we bring the 8 down next to the 4.
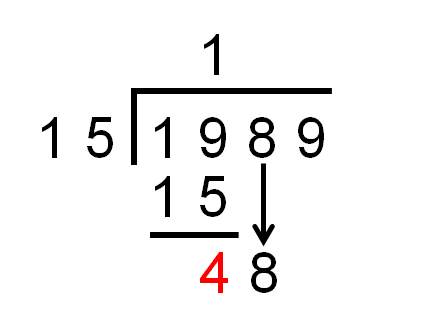
Then, we divide 48 ÷ 15 = 3 rem 3.
(Remember that 3 × 15 = 45 and so the remainder is 48 - 45 = 3.)
In long division, we bring the 9 down next to the 3.
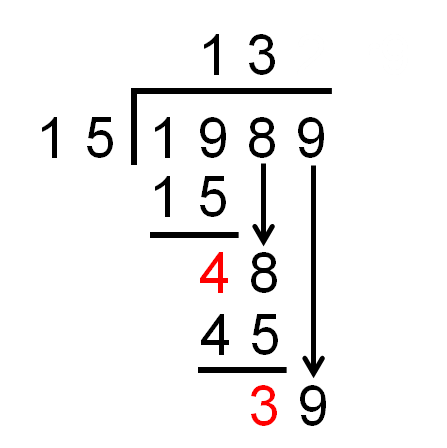
Lastly, we divide 39 ÷ 15 = 2 rem 9.
(Remember that 2 × 15 = 30 and so the remainder is 39 - 30 = 9.)
The final remainder is 9.

Compare this to short division.
.png)
We have shown that 1989 ÷ 15 = 132 r9
Hint
With long and short division, it helps to know the multiples of the number we are dividing by.
Here, it helped to know the multiples of 15 are 15, 30, 45, 60, 75, 90 etc.
When dividing by 14, it helps to know the multiples of 14 are 14, 28, 42, 56, 70, 84 etc.
Are you ready to have a go at the questions now?

We can look back at this example again at any point by clicking on the red help button on the screen.








