Calculate the Surface Area of a Cylinder

In this activity we will calculate the surface areas of cylinders.

Here is a cylinder. (It is very similar to a prism with a circular cross-section)

 

 

To find the surface area of this 3D shape we have see what the net looks like!

 

Its net is made up of two circles and a rectangle.

 

 

 To calculate the surface area, we need the area of the circle x 2 + area of rectangle

 

Area of circle

The area of a circle is πr² 

 

Area of Rectangle

Area = height x the circumference of a circle

Area = π x diameter x height

Area =  πd x H

 

 

Surface Area of a Cylinder

 

 

 

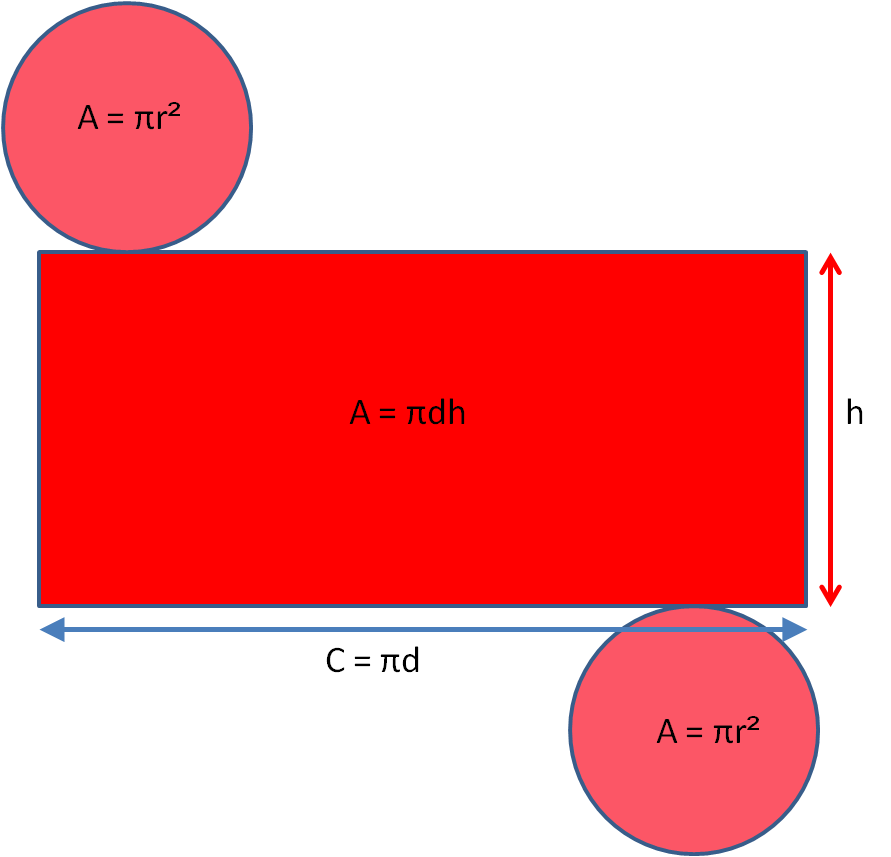
So the surface area is the area of the two circles + the area of the rectangle.

 

The area of the two circles = 2πr²

The area of the rectangle =  πdh  or we can write 2πrh (because the diameter is the radius x 2)

 Surface Area = 2πr² + πdh = 2πr² + 2πrh

 

Let's look at a typical question!

 

Example

Find the surface area of this cylinder in cm² to 1 decimal place.

 

 

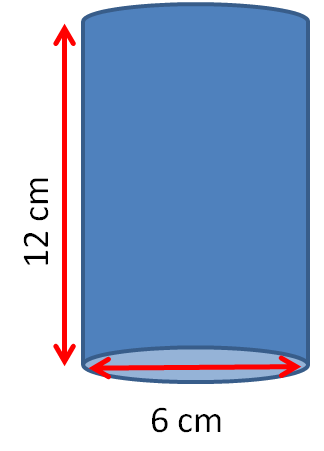
Answer

Diameter = 6 cm

Radius = 6 ÷ 2 = 3 cm

Height = 12 cm

 

Surface Area = 2πr² + 2πrh 

SA = 2 x π x 3² + 2 x π x 3 x 12

SA = 282.74

SA =  282.7 cm² (1 dp)

 

Let's do some questions!