Convert Fractions to Decimals

In this activity, we'll be converting fractions to decimals using both a calculator and some manual systems.

Sounds daunting - do not worry!

What do we actually mean when we write 1/2?  We can also say this as 1 ÷ 2 = 0.5, and just like that, we've converted a fraction into a percentage.

Obviously, there is a little bit more to it than that, but that's the basics.

Example 1

The fraction 2/10 means 2 ÷ 10 and is therefore 0.2 written as a decimal.

What about 3/20?  Well here, it's a good idea to get the fraction to a number we're happier dealing with.  We can multiply both the denominator and the numerator by the same number to help us here...

If we multiply 20 × 5 we have 100 as our denominator.  So, we do the same to the numerator 3 × 5 to get 15 and now we have 15/100

Now, all we need to do is to divide 15 by 100, and to do that we would move the decimal place 15.0 two places to the left and we have 0.15.
 

But, what do we do if we have a number that can't easily be changed so that the numerator is 100?  What about 2/7?

Example 2

This fraction seems a bit more of a challenge, so we can tackle it in one of two ways. It can be calculated immediately with a calculator, but can also be found manually by dividing.

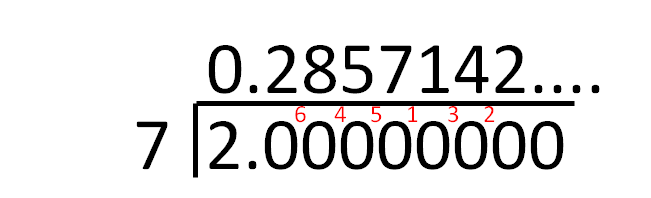
This shows that 2/7 as a decimal is 0.285714.....

This rounds to 0.2857 to 4 decimal places.