Calculate Lengths of Sides in Similar Triangles Using Scale Factors

Triangles that have exactly the same angles are similar.

 

If two angles match, the third angle will automatically also match as the angle sum is always 180º.

 

We can find similar triangles when a triangle is cut by a line parallel to the base, as in the example below:

 

 

 

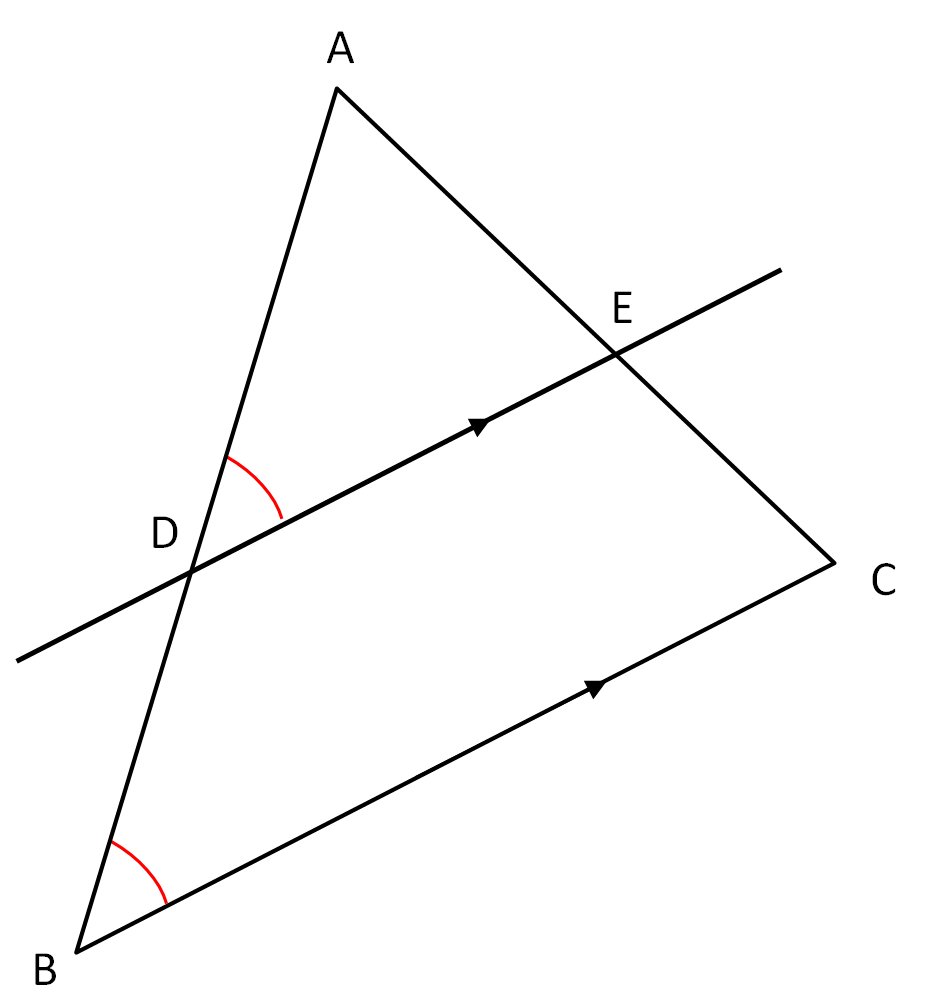
This is because the apex (top) angle is in both triangle ABC and in triangle ADE.

 

∠ABC = ∠ADE because they are corresponding angles on parallel lines.

 

The third angles automatically match, and therefore the triangles are similar.

 

We can separate the triangles to make the similar proportions easier to spot.

 

Triangle ABC is similar to Triangle ADE.

 

 

 

Example:

Find the value of y from the information given in this diagram.

 

 

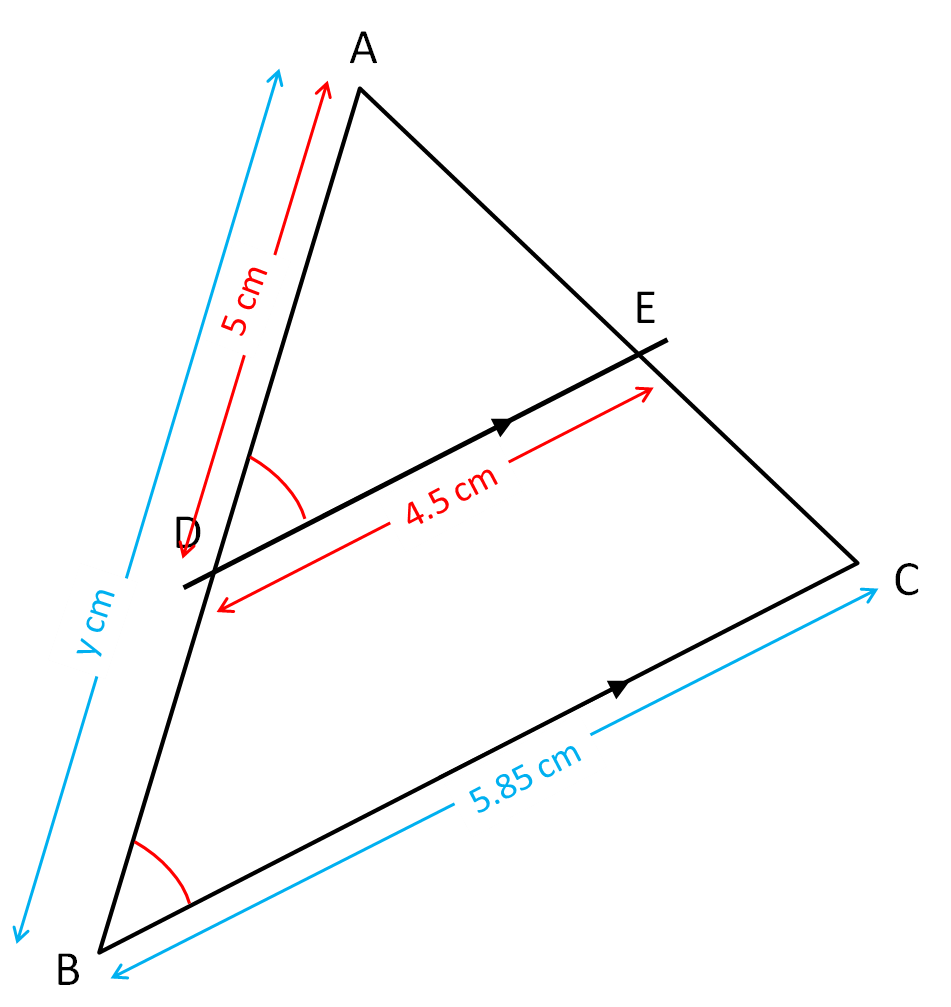
(Not to scale)

 

Answer:

The triangles are similar because two angles match, and so the third angle will too.

 

Comparing corresponding sides, we find that the scale factor is 5.85 ÷ 4.5 = 1.3

y = 1.3 × 5 = 6.5

 

Now, let's tackle some questions together!