Calculate Probability of Complementary Events Using Tables

We roll two dice and add what they land on. What could help us find the probability of getting a total of no more than 10?

 

       

 

Well, we could generate the whole sample space (i.e. all possible outcomes) using a table!

 

 

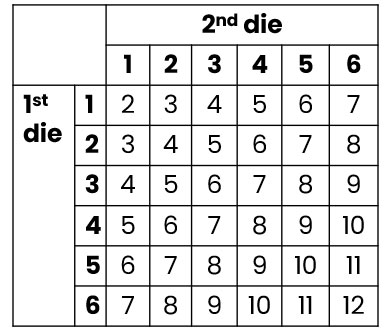
Rolling a die has 6 possible outcomes and we roll two of them, so there are 6 x 6 = 36 possible outcomes altogether.

 

From the table, we can count that a whopping 33 outcomes have a total of no more than 10!

 

This means that the probability of getting a total of no more than 10 is:

33/36 = 11/12

 

 

But generating the whole sample space is a bit tedious - is there a faster way to calculate the probability?

 

Well, yes, there is!

 

We have only two options when it comes to getting a total of no more than 10: either we get it or we don't.

 

Let's remember that the probability of something not happening is 1 minus the probability of it happening.

'Not getting a total above 10' is getting at least 11.

 

There are three ways of getting a sum of 11 or 12:

5 + 6 = 11

6 + 5 = 11

6 + 6 = 12

 

This is out of 6 x 6 = 36 possible outcomes altogether.

So, the probability of getting at least 11 (i.e. not getting at most 10) is:

3/36 = 1/12

 

That means the probability of getting at most 10 is:

1 - 1/12 = 11/12 which is exactly what we got before!

 

Wasn't listing the outcomes for getting at least 11 so much faster?!

 

 

Ready to put all this into practice?