Calculate Conditional Probability from Venn Diagrams

How could we use this Venn diagram to find the conditional probability that a randomly selected student goes to debating given that they go to chess? 

 

 

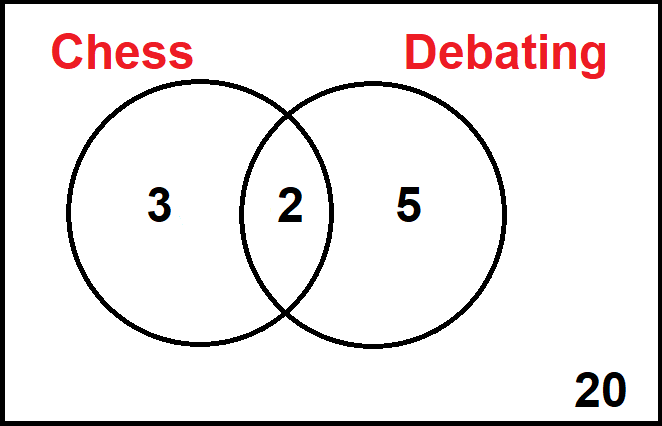
We know that conditional probability restricts the pool of students out of which we are choosing using the condition.

 

In this case, the condition is the student taking chess.

 

From the Venn diagram, we can see that 3 + 2 = 5 students go to chess.

So 5 is the number of possible outcomes for our conditional probability.

 

We want the probability that a student also goes to the debating club.

We can see that there are 2 students in the 'overlap', i.e. the intersection.

So 2 students is the number of desired outcomes for our conditional probability.

So 2 out of the 5 students who go to chess also go to debating.

 

That means the probability that a randomly selected student goes to debating given that they go to chess is 2/5!

 

If we call the sets of students who go to chess and debating C and D, respectively, then we can denote this probability using the symbol for given, i.e. the vertical line $|:$

$P(D$$|$$C)$$=\; 2/5$

 

 

Using the same Venn diagram, how could we find P(C$|$C $\cup \; D)?$

 

 

Oh wow, C$|$C $\cup \; D\; is$ a lot of symbols, isn't it?!

 

Let's decipher what it means:

C means goes to chess.

$|$means given.

∪ means union (the two circles together) so C ∪ D means goes to chess or debating (or both).

So P(C ∣ C ∪ D) means the probability that a randomly selected student goes to chess given that they go to chess or debating (or both).

 

$That\text{'}s\; not\; so\; awful,\; is\; it?!$

Here, we are restricted to the students in the union of C and D, i.e. those students who go to chess or debating (or both) - our condition.

 

 

We can see that there are 3 + 2 + 5 = 10 students in the two circles together.

So, C ∪ D = 10

 

There are 3 + 2 = 5 students who go to chess (and are still in our union).

So 5 out of the 10 students who $go\; to\; chess\; or\; debating\; (or\; both)$ go to chess.

 

P(C ∣ C ∪ D) = 5/10 = 1/2

 

Ready to put all this into practice?