Calculate Probability from Venn Diagrams

Do you go to any clubs at your school?

 

 

Year 9 students were asked what after-school club they go to: chess or debating.

 

The results are illustrated in the following Venn diagram:

 

 

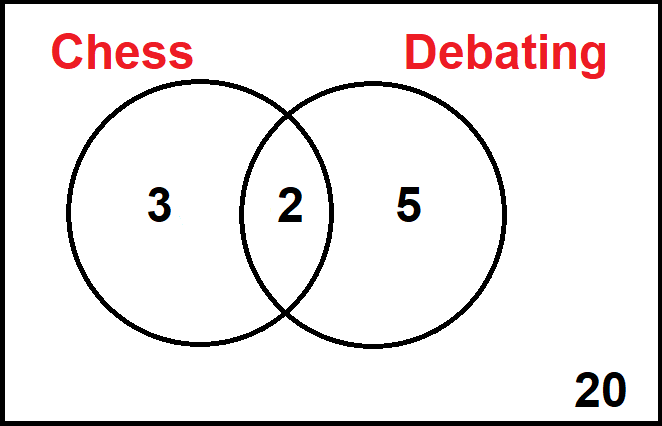
What is the probability that a student picked at random goes to both?

 

We can see that there are 2 students in the 'overlap', i.e. the intersection.

 

If we call the sets of students who go to chess and debating C and D, respectively, then we can denote it using $\cap :$

$C\; \cap \; D$$=\; 2$

 

There are 3 + 2 + 5 + 20 = 30 students altogether.

So the probability that a student picked at random goes to both clubs is:

P($C\; \cap \; D)\; =\; 2/30\; =\; 1/15$

 

 

Similarly, how could we find the probability that a student picked at random goes to chess or debating?

 

First things first!

In maths, when we say 'or', we don't mean 'either ... or ...'  we mean  '... or ... or both'.

This means that when we want students who go to chess or debating, we want those who go only to chess, only to debating or to both.

 

We call the set of these students the union (it is the two circles 'united' together!).

We denote this using the symbol ∪ (easy to remember - it looks a 'u' as in 'union'!).

 

So here we have:

C ∪ D = 3 + 2 + 5 = 10

 

So 10 out of 30 students go to chess or debating.

That means the probability that a student picked at random goes to chess or debating is:

P(C $\cup \; D$) = 10/30 = 1/3

 

 

Let's have a go at some questions!