Quadratics can be dealt with in two ways - algebraically and graphically.
A lot of students see these as two separate topics, however, they do cross over and you can use one technique when dealing with the other.
The significant points of a quadratic graph
All quadratic graphs have the same form, they look something like this:
For all quadratic graphs, there are three things you need to be able to find using an algebraic method - the roots, the y-intercept and the vertex.
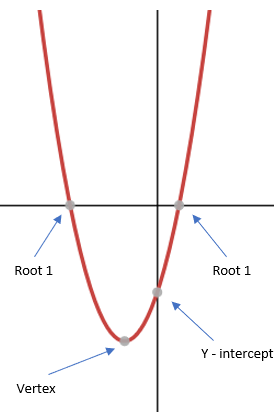
In this worksheet, we’re going to look at how we find the vertex (the turning point) algebraically.
Example:
How to find the coordinates of the vertex (turning point) for the quadratic y = x2 + 3x - 4
For this, we have to use one of the techniques for dealing with quadratics, completing the square.
Step 1: Complete the square for the quadratic
Using the technique of completing the square, we can see that:
y = x2 + 3x – 4 → y = (x + 1.5)2 – 6.25
Step 2: Find the x coordinate of the turning point
This relies on you knowing something about square numbers – they can never be negative.
The smallest a squared number can be is 0.
When we are looking for the vertex, we are looking for where the value of y is as low as possible (the minimum) - this happens when the squared bracket is zero.
So what value of x will make the squared bracket zero?
(x + 1.5)2 = 0
x + 1.5 = 0
x = -1.5
Step 3: Find the y coordinate of the turning point
We’ve already worked out that the minimum point is at x = -1.5.
To find the value of y, all we have to do is to plug x = -1.5 into the completed square y = (x + 1.5)2 – 6.25
If we do this, we get y = (-1.5 + 1.5)2 – 6.25
The bracket now becomes zero and leaves us with y = -6.25
This means that the coordinates of the vertex are (-1.5,-6.25)
Is the vertex always the lowest point?
No. If you have a graph of the form y = x2 + ax + b you will get a minimum, however if you have a graph of the form y = -x2 + ax + b, you will get a maximum.
Let's try some questions now.