A very common question type to see on GCSE exams are problems involving compound units related to speed, distance and time.
The most challenging element when completing questions about speed, distance and time is remembering the relevant formulae.
How to Remember the Formulae
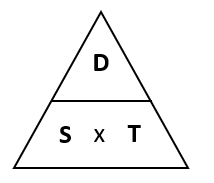
The easiest approach is to memorise the formulae triangle shown below, which we can then use to find the any single formula:
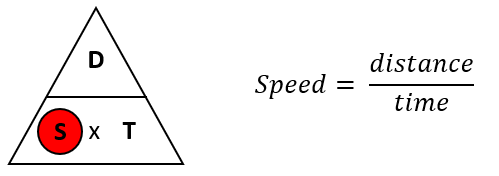
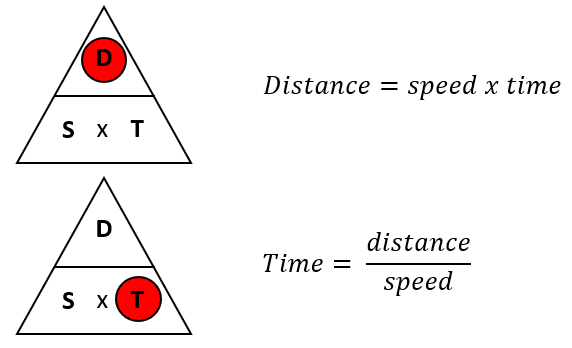
How To Use This Diagram
Simple, just highlight the element you are trying to find (we've done it with a red circle) and the formula to find this will use what's left:
Let's look at these formulae in action now.
e.g. A car travels at 40 mph for 3 hours. How far does it go?
The first step in these calculations is always to decide what we are trying to find.
For this one, we are asked "How far...?" so this must be a distance question:
D = S × T
Now we can simply plug our numbers into this formula:
D = 40 × 3 = 120
The last question that we need to ask ourselves is what the measurement units should be.
The trick here is that they are always the same as one of the other units.
The speed here is given in miles per hour, so the distance must be in miles.
So Distance = 120 miles
Let's try one more example to check we have these formulae clear in our mind.
e.g. A bike travels 100 m in 5 seconds. What is its average speed?
Once again, we need to decide which formula.
Don't worry that the question asks for average speed, we can still use the same formulae:
S = D ÷ T
Plugging in our numbers gives us:
S = 100 ÷ 5 = 20
Our original units were metres per second (remember, the units are in the question).
So Speed = 20 m/s
In this activity, we will use the Distance, Speed, Time formulae pyramid to identify which formula to use to find the answer to questions involving these three metrics using the methods shown above.