You may already feel confident with positive and negative index numbers, but we also need to be able to calculate powers represented as fractions.
If you are not feeling 100% about calculating positive and negative indices (e.g 34 or 5-2), it will be worthwhile revising these topics before trying this more challenging topic.
We need to be able to work with index numbers that are fractions. e.g. 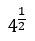 or
or .png)
If we look at the fractional indices in this table, we should spot patterns that will help us work out these values:
| e.g. 162 | 256 | The next step will be to divide our power by 2 (2 divided by 2 = 1). The next power we use will be 1. |
| 161 | 16 | 256 has been divided by 16, or we could say that we have found the square root of 256. (The next step will divide the power by 2 again. 1 divided by 2 is ½.) |
| 16½ | 4 | 16 has been divided by 4, or we could say that we have found the square root of 16. (The next step will again divide the power by 2 and ½ divided by 2 is ¼) |
| 16¼ | 2 | 4 has been divided by 2, or we could say that we have found the square root of 4. |
So 16½ means we have found the square root of 16 (i.e. the number that multiplied by itself will give us 16).
Let's look at another example now.
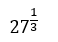 means that we need to find the cube root of 27.
means that we need to find the cube root of 27.
In simpler terms, we need to find the number that multiplied by itself 3 times gives 27.
The answer to this is 3.
This could be written as:
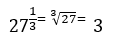
Here's one more example to check you've really got the hang of this.
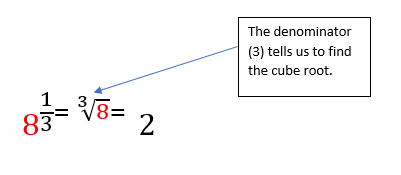
Let's try some questions now to put this into practise!
You may want to have a pen and paper so that you can compare your working to our explanations written by a teacher.







