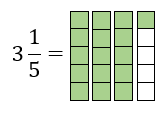When you are working with fractions, you will come across both top-heavy fractions (correctly called improper fractions) and mixed numbers.
Top-heavy fractions have larger numerators than denominators.
Mixed numbers describe expressions which use both whole numbers and fractions together.
You need to be able to convert between these two forms and identify equivalents.
e.g. Convert this mixed number into a top-heavy fraction:
| 3 |
|
If we draw this fraction using bars, we have three wholes and one fifth, like this:
If we count the shaded sections, we have 16 in total and each one is worth 1/5 so our fraction can now be written as:
| 16 |
| 5 |
Doing this the quicker way...
You should have noticed that the denominator is the same in both the question and answer fractions. This is ALWAYS true.
So we just need to find the numerator.
If we have 3 wholes which we are splitting into fifths, we have 3 x 5 = 15 fifths.
We need to remember that we had an extra 1 fifth in the question too, which gives us 16 overall.
To summarise:
In order to find the new numerator, multiply the whole number by the denominator then add the numerator.
The denominator will stay the same in both fractions.
In this activity, you will convert mixed numbers (so whole numbers and fractions) into top-heavy, improper fractions.
This is a very useful skill to use when adding or subtracting fractions.