Find Equivalent Fractions

Equivalents fractions are simply fractions that are equal.

 

The golden rule you must remember when you are manipulating fractions is that;

Whatever you do to the numerator, you must do the same to the denominator.

 

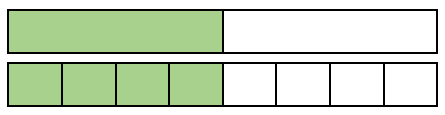
Imagine these fractions as bar models. 

1 2

=

4 8

 

 

Both have the same amount shaded so they must be equal.

 

Finding equivalent fractions

e.g. 

 

3 4

=

? 16

 

We need to notice that we have two denominators and we are missing a numerator.

The first denominator has been multiplied by 4 to become the second, so we must do the same for the numerator.

3 x 4 = 12

 

3 4

=

12 16

 

 

Simplifying a fraction

To simplify a fraction (make the numbers smaller), we have to find the highest common factor.

This is the largest number we can divide both numbers by.

When we have found this, we need to divide both the numerator and denominator by this amount. 

 

e.g. Simplify:

 

45

120

 

The highest common factor of these two numbers is 5, so we have to divide both numbers by 5:

45 120

=

45 ÷ 5 120 ÷ 5

=

9 20

 

In this activity, you will find equivalent fractions and simplify fractions into their lowest possible components.

Make sure you have your times tables and knowledge of factors at the ready to support you!