Oh yes.... the awkward one - the trapezium!

Where might you see a trapezium?
Trapeziums can be used in a lot of design or architectural work.
Don't be put off by the awkward shape.
The good news is that there is a formula to help us.
The bad news is that you have to learn it!
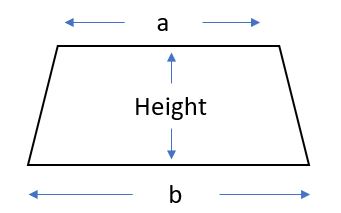
The confusing bit: (a + b) ÷ 2 x height This is the scary-looking formula often given at the front of an exam paper.
The easy bit is that the a and b just need to be substituted for numbers: (top length + bottom length) ÷ 2 x height.
.png)
The area of this trapezium is:
6 + 12 = 18
18 ÷ 2 = 9
9 x 8 = 72 cm²
This will soon become second nature.
Remember when working with area, we always answer in units squared.

Now you could go barking up the wrong tree so be careful.
When you are given measurements for a trapezium, you are sometimes given the top, bottom, vertical height and a slanted height.
You always want the vertical height as shown in the diagram above.
Once you have learned the formula you are flying.