Link Inputs and Outputs

Functions are rules that link inputs and outputs.

In a function, each input has only one corresponding value as an output.

Here is an example of a function with a rule times by 2:

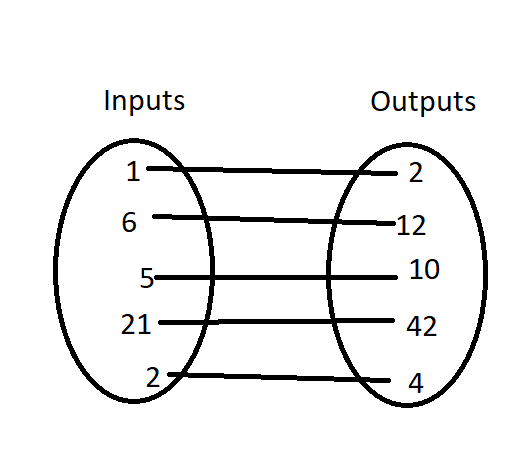
However, the picture below does not show a function, just a relationship between numbers:

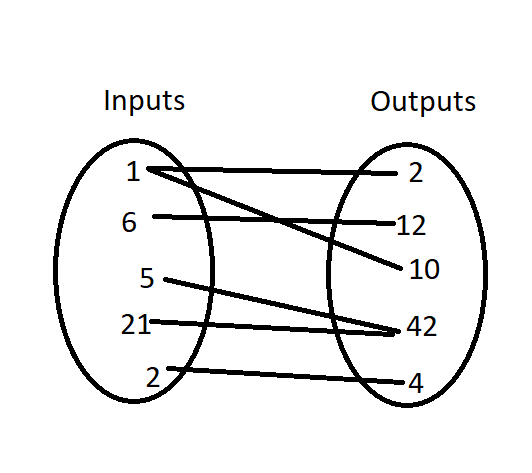
This is because 1 is linked with two outputs, and in functions, each input must have only one corresponding output.

In this activity, we will identify functions accurately and use function relationships to find missing inputs or outputs.