Solve Inequalities (on a number line)

When we are working with inequalities, a common question to be asked is to state all the numbers that satisfy an inequality.

We can either do this by giving a solution set or by drawing the numbers on a number line.

In this activity, we are going to focus on the second option here of representing inequalities on a number line.

 

 

e.g. Illustrate the inequality 3x – 4 > 2 on a number line.

 

The first step here is to solve the inequality:

3x – 4 + 4 > 2 + 4

3x > 6

3x ÷ 3 > 6 ÷ 3

x > 2

 

Now we have our solution set, we can draw this on a number line.

 

As the inequality uses a greater than sign, we use an unshaded circle to show the value of 2.

We know that the viable solutions must be greater than 2, so we draw an arrow to the right, like this:

 

 

 

 

Let's try another now.

 

e.g. Illustrate the inequality 2x + 1 ≤ 5 on a number line.

 

The first step here is to solve the inequality:

2x + 1 ≤ 5

2x + 1 -1 ≤ 5 - 1

2x ≤ 4

2x ÷ 2 ≤ 4 ÷ 2

x ≤ 2

 

Now we have our solution set, we can draw this on a number line.

 

As the inequality uses a less than or equal to sign, we use a shaded circle to show the value of 2.

We know that the viable solutions must be less than or equal 2, so we draw an arrow to the left, like this:

 

 

 

 

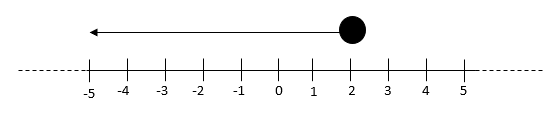
Let's practise one more before we try the activity; this time using a inequality with three parts.

 

e.g. Illustrate the inequality -1 ≤ 2x – 3 < 5 on a number line.

 

The first step here is to solve the inequality:

-1 + 3 ≤ 2x – 3 + 3 < 5 + 3

2 ≤ 2x < 8

2 ÷ 2  ≤ 2x ÷ 2  < 8 ÷ 2

1 ≤ x < 4

 

Now we have our solution set, we can draw this on a number line.

 

We can see that the viable solutions must be between 1 and 4.

The circle at 1 has to be shaded (as it has a ≤ sign) and the one at 4 (as it has a < sign) has to be unshaded, like this:

 

 

 

 

In this activity, you will revise and apply the rules for illustrating solution sets for inequalities as well as identifying the correct illustrations to represent inequalities. 

 

You will not be required to actually draw any number lines in this activity to reach the correct answers, unless you choose to. 

However, once you have completed this activity, you may want to go back through each question and draw number lines to represent some of the inequalities shown here so that you can practise this skill further.