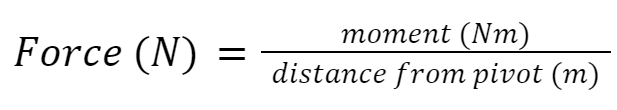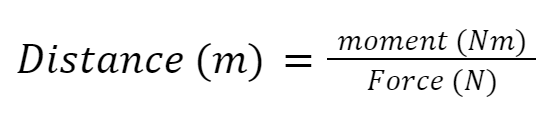Calculate Moments

We use spanners to help us unscrew large bolts. Imagine if you had to unscrew a bolt with your bare hands - it would be much harder. Do you know why that is?

 

 

The length of the spanner provides a greater turning force on the bolt. This turning effect is called a moment.  A spanner can provide a much greater turning force because of its length.

 

Let's learn more about moments, and how to calculate them!

 

Turning forces always act at a certain distance from a pivot. For a spanner, the pivot would be at the bolt. 

You can calculate the moment using this equation:

 

moment (Nm) = force (N) × distance from pivot (m)

 

The standard unit for moment is Nm, but sometimes we use Ncm instead, depending on the question. 

 

Let's look at an example. 

 

Example 1

You apply a force of 15 Newtons on a door, and you apply that force at a distance of 0.7 metres from the hinges (the pivot). What is the moment?

 

 

Answer 

Let's substitute the values into the equation.

moment (Nm) = 15 N × 0.7 m = 10.5 Nm

 

We can rearrange the equation, to make force or distance the subject. 

 

 

 

Example 2

 A person sits on a see-saw and causes a moment of 300 N. Their distance to the pivot was 1.5 metres. What force did they exert?

 

 

Answer

We need to choose the correctly rearranged equation:

Force (N) = moment (Nm) ÷ distance (m)

Force (N) = 300 ÷ 1.5

Force (N) = 200 N

 

Next, we are going to learn about the law of moments.

Imagine that you sit on a see-saw with a friend on the other side. If you sit in the right positions, the see-saw will balance, even if you don't have the same weight as your friend. 

The moment caused by you is equal to the moment caused by your friend, and so you and your friend (and the see-saw) are in equilibrium!

 

Here is another example. 

 

 

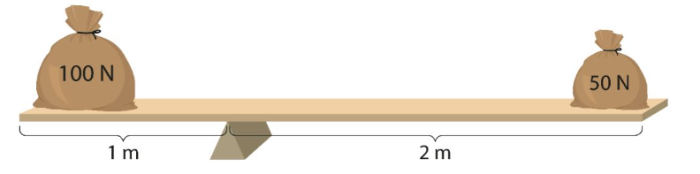
The bag on the left side of the pivot causes an anticlockwise moment.

The bag on the right side of the pivot causes a clockwise moment. 

 

The law of moments says that an object is in equilibrium (it balances) if the total clockwise moment is equal to the total anticlockwise moment. 

For the example above:

Anticlockwise moment = 100 N × 1 m = 100 Nm

Clockwise moment = 50 N × 2 m - 100 Nm

 

So it is in equilibrium!

 

Now that we understand moments a little better, let's try some practice questions!