EdPlace's KS3 home learning maths lesson: Finding the Angle Sum in a Regular Polygon

Looking for short lessons to keep your child engaged and learning? Our experienced team of teachers have created English, maths and science lessons for the home, so your child can learn no matter where they are. And, as all activities are self-marked, you really can encourage your child to be an independent learner.

Get them started on the lesson below and then jump into our teacher-created activities to practice what they've learnt. We've recommended five to ensure they feel secure in their knowledge - 5-a-day helps keeps the learning loss at bay (or so we think!).

Are they keen to start practising straight away? Head to the bottom of the page to find the activities.

Now...onto the lesson!

Key Stage 3 statutory requirements for maths

Year 8 students should be able to calculate the sum of angles in a triangle and use it to deduce the angle sum in any polygon and to derive properties of regular polygons.

Picturing Polygons...

What is a polygon? (it’s not a missing parrot!) When was the last time that you needed to work out an interior or exterior angle of one of these shapes? For the average UK parent, it’s probably been a little while, and the concepts and terminology in this topic can seem obtuse!

We're confident that if you follow the step-by-step approach below your child will be able to:

1) Understand how to find the sum of the angles in a polygon

2) Apply this knowledge to solve problems

3) Explain their reasoning clearly

Terrified of the Terminology?

Before you begin, it helps for students to know how we define the key quantities that we will be discussing.

A polygon is simply a two dimensional (or flat) shape made from straight lines. So a triangle is a polygon with 3 sides, and a square or rectangle is a polygon with 4 sides. A circle is not a polygon as it has one curved side. Here are some more polygons with more sides and the names we can use to describe them.

Pentagon - 5 sides

Hexagon Hexagon - 6 sides

Heptagon or Spetagon Heptagon/Septagon - 7 sides

Octagon Octagon - 8 sides

Decagon Decagon - 10 sides

All of these names should be familiar to your child, but it's worth just checking! How many of these names were familiar to you? Do you know how many sides in a triskaidecagon or enneadecagon? Don’t worry you probably don’t need to know, unless you’re a fan of general knowledge quizzes! (13 and 19, if you're really interested!)

Step 1 - Checking Prior Knowledge

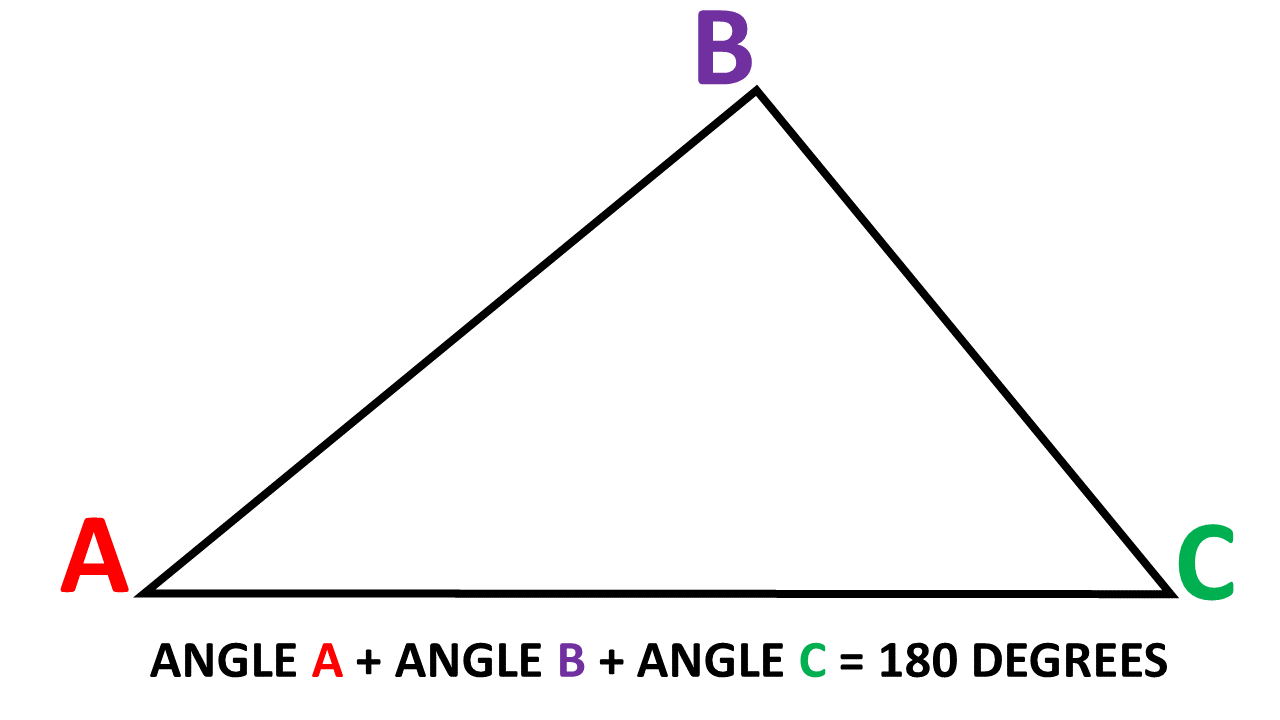
It's always worth recapping content with students before building on a topic. They should be comfortable with these two concepts, but if they're not it's not a problem, just start here first! 1) A regular polygon is a polygon where all the sides are an equal length. This means that all the individual angles at the corners (or vertices) of the shape will be the same. 2) The 3 angles inside a triangle add to 180 degrees.

Being able to find the angle sum in a polygon relies on the knowledge that the 3 angles inside a triangle add to 180 degrees.

Angles in a Triangle

Step 2 - The Difference Between Interior and Exterior Angles

Children should also be able to identify the interior and exterior angles of shapes. Interior angles, as their name suggests are the angles found inside a shape, and are measured as the amount of turn from one side to the next side of the shape while inside the polygon. Exterior angles are the amount of turn from one side to the next but measured on the outside of a shape. As the exterior and interior angles are on a straight line the number of degrees adds to 180.

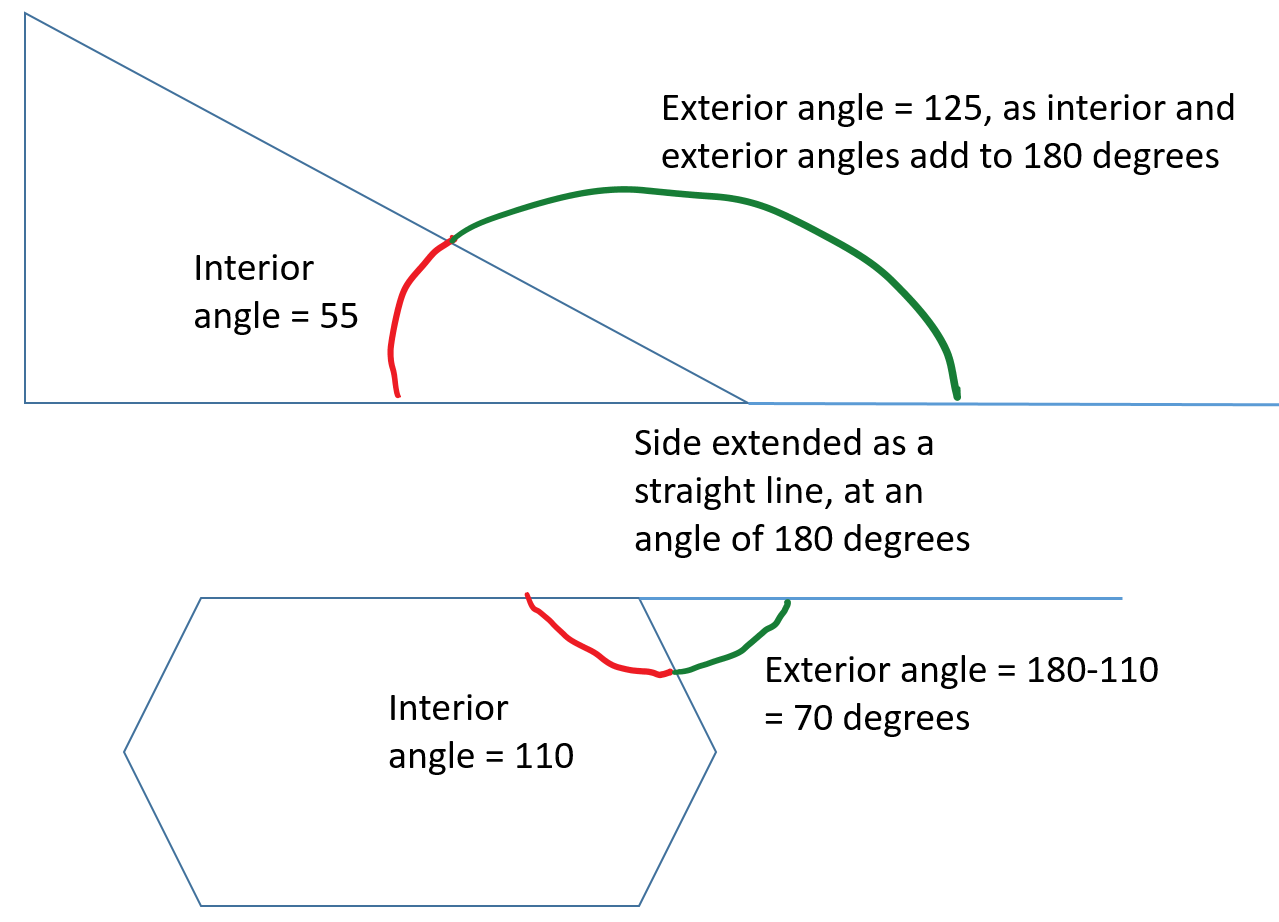
Interior and Exterior Angles

Step 3 - Converting Between Percentages and Decimals

We’ll now start to think about finding the total of interior angles of a polygon. The key to this is visualising the number of triangles that can be drawn inside a polygon. This rectangle can be split into 2 triangles, each containing 180 degrees. So the interior angles of a rectangle add to 2 x 180 = 360. We know this is true, as each of the 4 angles of a rectangle has to be a right angle of 90 degrees. 4 x 90 also = 360.

Triangles in a Rectangle

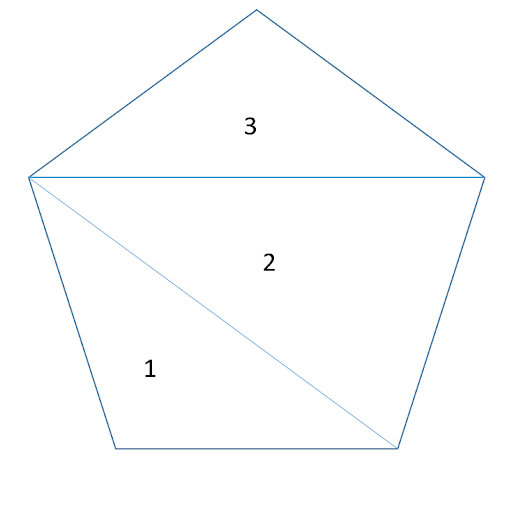
Now let’s look at a pentagon with 5 sides. By drawing from one vertex (or corner) to each opposite vertices in turn we can split the shape into 3 triangles. The angle sum for a pentagon is 3 x 180 = 540 degrees

Triangles in a Pentagon

The hexagon has 6 sides. It has been divided into 4 triangles, and 4 x 180 = 720. The interior angle sum of a hexagon is 720.

Triangles in a Hexagon

Hopefully, your child can see that there is a bit of a pattern developing here? What calculation could we use to work out the total sum of angles inside a polygon? If we start with the number of sides and subtract 2, we will find the number of triangles in the shape. This is because we need 2 sides to make the first triangle. We can then multiply this number by 180 to find the angle sum inside the shape.

(Number of Sides - 2) × 180 = Total Sum of Interior Angles

With this logic, you can ask your child to create a table with the following headings... 'Number of Sides' 'Number of Triangles inside' and 'Total Sum of Interior Angles' for the following polygons - Heptagon, Octagon, Decagon.

Step 4 - Polygons in Practice!

Why not apply this understanding to the following sums together?

What is the interior angle sum of a decagon (10 sided shape)?
What is the angle sum in a 20 sided shape?
What is the angle sum in a 40 sided shape?

And how about these challenge questions...

If a regular polygon has equal sides and therefore equal angles, and you know the angle sum of a 12 sided shape is 1800, can you work out the size of one interior angle?
Can you find the size of one interior angle of a 60 sided shape? Imagine drawing this with a protractor... nightmare!
Think about a 600 sided shape- what would its interior angle be? How could you draw this shape? Is there another shape that you could use as an approximation?

Step 5 - Give it a go...

Now see if you can tackle these activities!

All activities are created by teachers and automatically marked. Plus, with an EdPlace subscription, we can automatically progress your child at a level that's right for them. Sending you progress reports along the way so you can track and measure progress, together - brilliant!

Activity 1 - Calculating Angles at a Point and on a Straight Line

Activity 2 - Interior Angle Sums

Activity 3 - Interior Angles of Regular Polygons

Activity 4 - Exterior Angles of Regular Polygons

Activity 5 - Interior and Exterior Angles of Regular Polygons

Answers