
EdPlace's GCSE home learning maths lesson: Surface Area
Looking for short lessons to keep your child engaged and learning? Our experienced team of teachers have created English, maths and science lessons for the home, so your child can learn no matter where they are. And, as all activities are self-marked, you really can encourage your child to be an independent learner.
Get them started on the lesson below and then jump into our teacher-created activities to practice what they've learnt. We've recommended five to ensure they feel secure in their knowledge - 5-a-day helps keeps the learning loss at bay (or so we think!).
Are they keen to start practising straight away? Head to the bottom of the page to find the activities.
Now...onto the lesson!
We're Scratching More Than The Surface With This Topic!
You spent hours choosing the perfect present for your child. You wrapped it up carefully and were so excited to give it to them on their birthday and …… drum roll…… they were more interested in the box it came in. How often did that happen when they were younger? Little did you know, that at a young age they were taking an interest in maths and surface area! Now that they're that bit older they need to be able to demonstrate an understanding of this childhood pastime.
We're confident that if you follow the step-by-step approach below your child will be able to:
1) Recall the different formulae required to find the surface area of any shape
2) Apply this knowledge to solve problems
3) Explain their reasoning clearly
Finding the Right Formula
To get started we need to know the formulae for finding the area of certain shapes. It's important to check that your child knows them as only the more complex ones are given on an exam paper. These formulae are just something your child will have to learn. Why not try this first part as a quiz to assess your child’s current understanding. They might surprise you with what they know!
Area of a square = base x height
Area of a rectangle = base x height
Area of a parallelogram = base x height (nothing like a bit of repetition).
Area of a triangle = base x height ÷ 2 (or ½ base x height)
Note: The height is the vertical height of the triangle, not the slant height.
Area of a trapezium = top + bottom ÷ 2. Then multiply by the height. (Vertical height).
Area of a circle =πr² sometimes written as x radius x radius.
Circumference = π x diameter (Cherry Pies are Delicious)
Area = π r² (Apple Pies aRe Too)
Once your child knows these, all the hard work is done and makes what looks to be tricky on the 'surface' nothing more than a walk in the park. There are other surface area formulae that you child will need to be familiar with, like, the area of a cylinder, but these types of formulae are usually given on an examination paper.
Step 1 - Using the (not so) Secret Formula
Next check that your child understands what area is and can apply the correct formula. Area is the measurement of a given surface and is always measured in units squared. Therefore, the area of any 2D shape is the amount of space inside the boundary lines. Read on to see the formulae in action, you'll notice that we always include the correct units.
The area of a square with 4 cm sides is 4 x 4 =16 cm²
The area of a triangle of base 8 cm and vertical height 7 cm is 8 x 7 = 56 cm ÷ 2 = 28 cm². A common mistake here is that students forget to divide by 2
The area of a trapezium with the top length of 7 cm, the bottom length of 13 cm and a height of 8 cm 7 + 13 = 20 20 ÷ 2 = 10 10 x 8 = 80 cm²
The area of a circle with a radius of 4 cm π (or 3.14) x 4 x 4 = 50.24 cm²
That is all very well, I hear you ask but how can I explain surface area?
Step 2 - Seeing in 3D...
Now the fun begins! You need to apply the formulae learnt above to find the area of 3D shapes. As with any maths question encourage your child to break it down into smaller chunks. Always write down the answers as you go, students often try to retain all the information in their head until the last minute and this is where mistakes are made! Let’s look at the surface area of a cube. As you work through this problem with your child ask them what it is they already know. Hopefully, they can come up with the following:
1) Define area
2) They can see that a cube has all square faces
3) Bonus point is that all the faces will be the same size.
4) The area of a square is base x height
The surface area of any shape is the area of each face worked out and then added together. You can demonstrate this really easily if you have a dice to hand. For example, a cube has a side of 5 cm. First, calculate the area of 1 face 5 x 5 = 25 cm². Secondly, as a cube has 6 sides that are all equal multiply 25 cm² x 6 = 150 cm².
Step 3 - Starting to Take Shape!
In this next example we'll be using the formula that we're now confident with but this time we're working out the surface area of a rectangular prism. Again, if you want to really bring this to life look around for any kind of box in your house!
Hopefully, we can see what we need to do here, we know the formula for working out the area of a 2D rectangle, the only thing that is quite different is that this time all of the faces (surfaces) are not the same length. So, we need to consider this when we calculate the surface area.
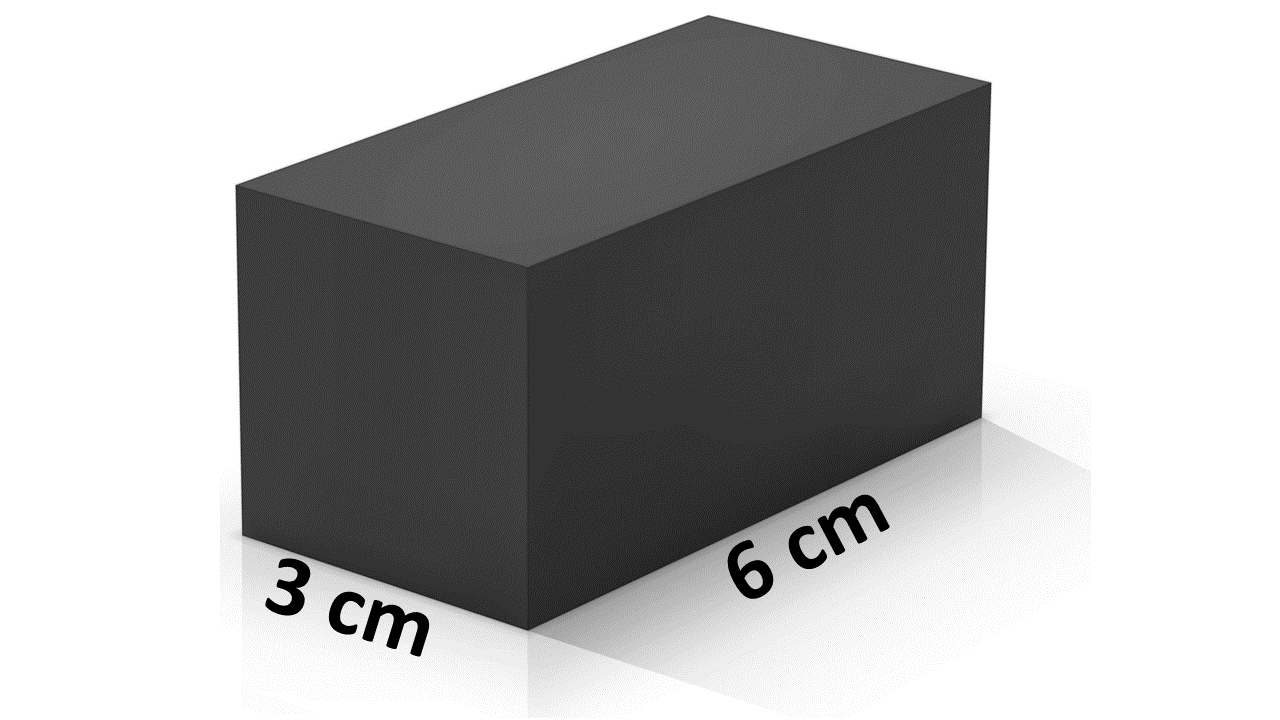
The area of the square face = 3 x 3 = 9 cm² and there are 2 of these faces = 9 cm² x 2 = 18 cm²
The area of the rectangular face = 3 x 6 = 18 cm² and there are 4 of these faces = 18 cm² x 4 = 72 cm²
Finally, we add this together and we know that the surface area of this rectangular prism = 18 cm² + 72 cm² = 90 cm²
This next question requires the same approach. We need to consider the number of faces and how they differ from one another in their area, before adding these figures altogether.
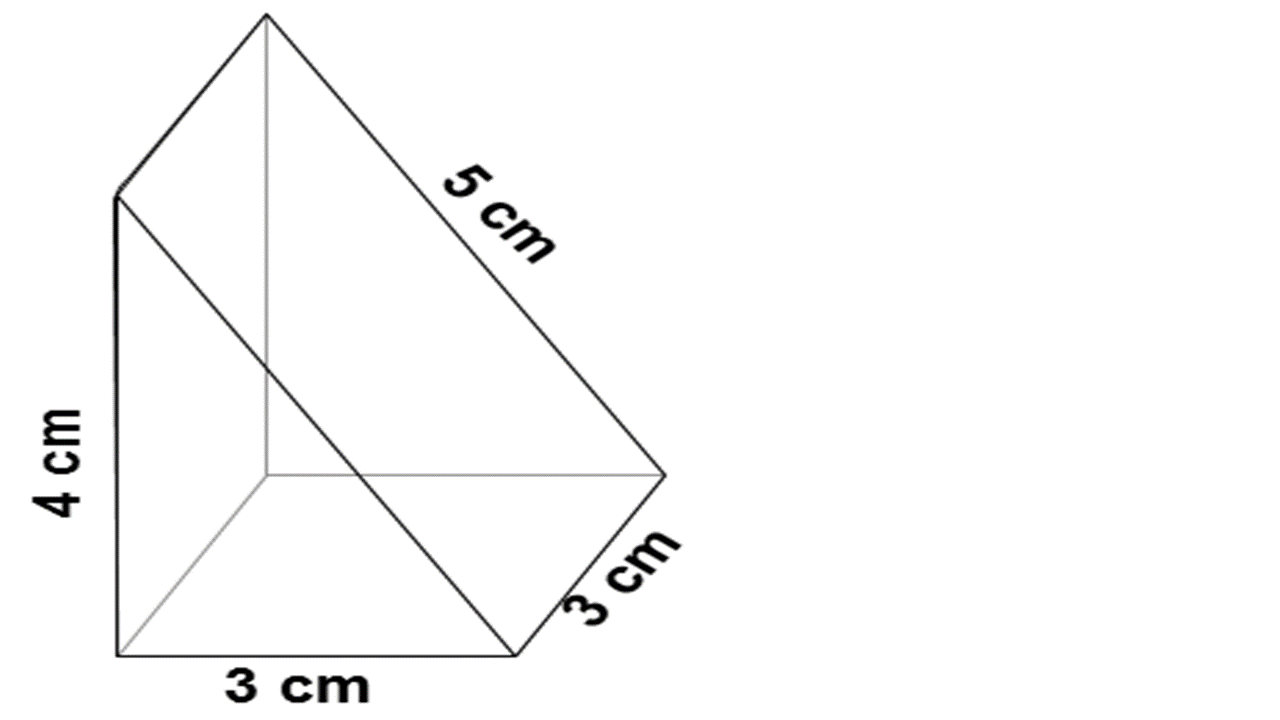
There are 5 faces in this triangular prism.
Let's start with the square face at the bottom 3 cm x 3 cm = 9 cm²
Let's now calulare the slanting face area 3 cm x 5 cm = 15 cm²
The upright rectangular face we know is 3 cm x 4 cm = 12 cm²
The triangular surface is (3 cm x 4 cm) ÷ 2 = 6 cm² and we know there are two of these faces so 6 cm² x 2 = 12 cm²
Now, we add these numbers up and get 9 + 15 + 12 + 12 = 48 cm²
Step 4 - Surface Area in Practice!
Before moving on to more complex problems it is always worth consolidating what you've covered with your child.
1) What is the formula for finding the area of a triangle?
2) What is the formula for finding the area of a circle?
3) What is the formula for finding the area of a trapezium?
4) What is meant by surface area?
5) What is the value of π (Pi)?
Step 5 - Give it a go...
Check your child’s progress and enhance their knowledge of surface area with the following activities.
The links below will guide you through the surface area of more complex shapes.
All activities are created by teachers and automatically marked. Plus, with an EdPlace subscription, we can automatically progress your child at a level that's right for them. Sending you progress reports along the way so you can track and measure progress, together - brilliant!
Activity 1 - Surface Area of a Cuboid
Activity 2 - Surface Area of Cylinders
Activity 3 - Find the Surface Area of a Pyramid
Activity 4 - Surface Area of a Cone
Activity 5 - Surface Area of a Sphere
Answers
1) Base x height ÷ 2
2) π x radius x radius (or πr2)
3) Top + bottom ÷ 2 x height
4) The area of every face of a 3D shape added together.
5) 3.14
Keep going! Looking for more activities, different subjects or year groups?
Click the button below to view the EdPlace English, maths, science and 11+ activity library








