Find the Surface Area of a Cone

Where is the best place to store ice cream cones? Conetainers....... Sorry!

 

 

 

Cone shapes are awkward, and one of the key things you could be asked is to find its surface area.

To find that, we need a formula.

 

First, there is some key information that you need to be aware of.

 

You will need to work with a slanted height shown as l in the formula.

You will need to work with π so the value of 3.142 or 3.14 can be used.

For these types of questions, using a scientific calculator is best as the value of π is decided for you.

 

You need to work with the radius, which is the distance from the centre of a circle to the edge.

Area is always measured in units²

 

 

 Nay bother.  

The formula comes in three stages:

 

1.  To find the area of the curved face, the formula is π x r x l

 

2. To find the area of the base the formula is π x r²

 

3.  Just add your answers together.

   π x r x l 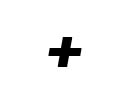 π x r²  

 

It can be a bother having to learn so many formulas (or formulae), so let us look at this closely.

 

A cone has a circular shape, so we need to use the formula for finding an area of a circle:  π x r²

This gives us the area of the surface of the base.

 

The other part of the formula starts the same and uses the radius, so the only other thing to think about is selecting (l) the slant height.

Question setters often give a vertical and a slant height, so beware.  Think that a cone slants. 

 

Let's get started.

 

 

Find the surface area of this cone.  The radius is 4 cm. The slant height is 7 cm.

 

Part 1

π x r x l 

π x 4 x 7 = 87.96 cm²

 

Part 2

π x r x r 

π x 4 x 4 = 50.27 cm²

 

Part 3

87.96 + 50.27 = 138.23 cm²

 

Just beware though, because sometimes you are given the diameter of the cone - remember to halve it to get the radius.